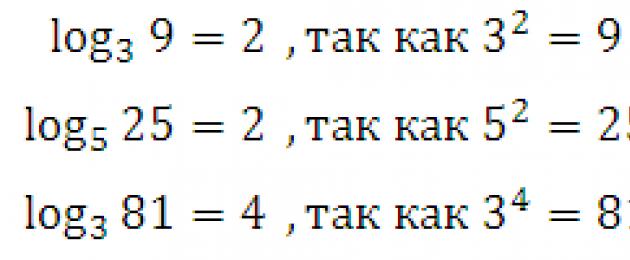Η διατήρηση του απορρήτου σας είναι σημαντική για εμάς. Για το λόγο αυτό, έχουμε αναπτύξει μια Πολιτική Απορρήτου που περιγράφει τον τρόπο με τον οποίο χρησιμοποιούμε και αποθηκεύουμε τις πληροφορίες σας. Διαβάστε τις πρακτικές απορρήτου μας και ενημερώστε μας εάν έχετε ερωτήσεις.
Συλλογή και χρήση προσωπικών πληροφοριών
Οι προσωπικές πληροφορίες αναφέρονται σε δεδομένα που μπορούν να χρησιμοποιηθούν για την αναγνώριση ή επικοινωνία με ένα συγκεκριμένο άτομο.
Ενδέχεται να σας ζητηθεί να δώσετε τα προσωπικά σας στοιχεία ανά πάσα στιγμή όταν επικοινωνήσετε μαζί μας.
Ακολουθούν ορισμένα παραδείγματα των τύπων προσωπικών πληροφοριών που ενδέχεται να συλλέγουμε και πώς μπορούμε να χρησιμοποιήσουμε αυτές τις πληροφορίες.
Ποιες προσωπικές πληροφορίες συλλέγουμε:
- Όταν υποβάλλετε μια αίτηση στον ιστότοπο, ενδέχεται να συλλέξουμε διάφορες πληροφορίες, όπως το όνομά σας, τον αριθμό τηλεφώνου, τη διεύθυνση email σας κ.λπ.
Πώς χρησιμοποιούμε τα προσωπικά σας στοιχεία:
- Οι προσωπικές πληροφορίες που συλλέγουμε μας επιτρέπουν να επικοινωνήσουμε μαζί σας με μοναδικές προσφορές, προσφορές και άλλες εκδηλώσεις και επερχόμενες εκδηλώσεις.
- Από καιρό σε καιρό, ενδέχεται να χρησιμοποιήσουμε τα προσωπικά σας στοιχεία για να στείλουμε σημαντικές ειδοποιήσεις και επικοινωνίες.
- Ενδέχεται επίσης να χρησιμοποιήσουμε προσωπικές πληροφορίες για εσωτερικούς σκοπούς, όπως διεξαγωγή ελέγχων, ανάλυση δεδομένων και διάφορες έρευνες, προκειμένου να βελτιώσουμε τις υπηρεσίες που παρέχουμε και να σας παρέχουμε συστάσεις σχετικά με τις υπηρεσίες μας.
- Εάν συμμετέχετε σε κλήρωση, διαγωνισμό ή παρόμοια προσφορά, ενδέχεται να χρησιμοποιήσουμε τις πληροφορίες που παρέχετε για τη διαχείριση τέτοιων προγραμμάτων.
Αποκάλυψη πληροφοριών σε τρίτους
Δεν αποκαλύπτουμε τις πληροφορίες που λαμβάνουμε από εσάς σε τρίτους.
Εξαιρέσεις:
- Εάν είναι απαραίτητο - σύμφωνα με το νόμο, τη δικαστική διαδικασία, σε νομικές διαδικασίες και/ή βάσει δημόσιων αιτημάτων ή αιτημάτων από κυβερνητικές αρχές στην επικράτεια της Ρωσικής Ομοσπονδίας - να αποκαλύψετε τα προσωπικά σας στοιχεία. Ενδέχεται επίσης να αποκαλύψουμε πληροφορίες σχετικά με εσάς εάν κρίνουμε ότι αυτή η αποκάλυψη είναι απαραίτητη ή κατάλληλη για λόγους ασφάλειας, επιβολής του νόμου ή άλλους σκοπούς δημόσιας σημασίας.
- Σε περίπτωση αναδιοργάνωσης, συγχώνευσης ή πώλησης, ενδέχεται να μεταφέρουμε τις προσωπικές πληροφορίες που συλλέγουμε στον αντίστοιχο τρίτο διάδοχο.
Προστασία προσωπικών πληροφοριών
Λαμβάνουμε προφυλάξεις - συμπεριλαμβανομένων διοικητικών, τεχνικών και φυσικών - για την προστασία των προσωπικών σας δεδομένων από απώλεια, κλοπή και κακή χρήση, καθώς και από μη εξουσιοδοτημένη πρόσβαση, αποκάλυψη, τροποποίηση και καταστροφή.
Σεβασμός του απορρήτου σας σε εταιρικό επίπεδο
Για να διασφαλίσουμε ότι τα προσωπικά σας στοιχεία είναι ασφαλή, κοινοποιούμε τα πρότυπα απορρήτου και ασφάλειας στους υπαλλήλους μας και εφαρμόζουμε αυστηρά τις πρακτικές απορρήτου.
Λογαριθμικές εκφράσεις, επίλυση παραδειγμάτων. Σε αυτό το άρθρο θα εξετάσουμε προβλήματα που σχετίζονται με την επίλυση λογαρίθμων. Οι εργασίες θέτουν το ερώτημα εύρεσης της σημασίας μιας έκφρασης. Πρέπει να σημειωθεί ότι η έννοια του λογάριθμου χρησιμοποιείται σε πολλές εργασίες και η κατανόηση της σημασίας της είναι εξαιρετικά σημαντική. Όσον αφορά την Ενιαία Κρατική Εξέταση, ο λογάριθμος χρησιμοποιείται κατά την επίλυση εξισώσεων, σε εφαρμοσμένα προβλήματα, καθώς και σε εργασίες που σχετίζονται με τη μελέτη συναρτήσεων.
Ας δώσουμε παραδείγματα για να κατανοήσουμε την ίδια την έννοια του λογάριθμου:


Βασική λογαριθμική ταυτότητα:

Ιδιότητες των λογαρίθμων που πρέπει πάντα να θυμόμαστε:

*Ο λογάριθμος του γινομένου είναι ίσος με το άθροισμα των λογαρίθμων των παραγόντων.
* * *

*Ο λογάριθμος ενός πηλίκου (κλάσματος) ισούται με τη διαφορά μεταξύ των λογαρίθμων των παραγόντων.
* * *
![]()
*Ο λογάριθμος ενός εκθέτη είναι ίσος με το γινόμενο του εκθέτη και του λογάριθμου της βάσης του.
* * *

*Μετάβαση σε νέα βάση
* * *
Περισσότερες ιδιότητες:

* * *
Ο υπολογισμός των λογαρίθμων σχετίζεται στενά με τη χρήση των ιδιοτήτων των εκθετών.
Ας παραθέσουμε μερικά από αυτά:
Η ουσία αυτής της ιδιότητας είναι ότι όταν ο αριθμητής μεταφέρεται στον παρονομαστή και αντίστροφα, το πρόσημο του εκθέτη αλλάζει στο αντίθετο. Για παράδειγμα:

Συμπέρασμα από αυτό το ακίνητο:
* * *
![]()
Όταν αυξάνεται μια ισχύς σε μια ισχύ, η βάση παραμένει η ίδια, αλλά οι εκθέτες πολλαπλασιάζονται.
* * *
Όπως είδατε, η ίδια η έννοια του λογάριθμου είναι απλή. Το κύριο πράγμα είναι ότι χρειάζεστε καλή πρακτική, η οποία σας δίνει μια συγκεκριμένη ικανότητα. Φυσικά απαιτείται γνώση τύπων. Εάν η ικανότητα μετατροπής στοιχειωδών λογαρίθμων δεν έχει αναπτυχθεί, τότε κατά την επίλυση απλών εργασιών μπορείτε εύκολα να κάνετε ένα λάθος.
Εξασκηθείτε, λύστε πρώτα τα πιο απλά παραδείγματα από το μάθημα των μαθηματικών και μετά προχωρήστε σε πιο σύνθετα. Στο μέλλον, θα δείξω σίγουρα πόσο «τρομακτικοί» λογάριθμοι δεν θα εμφανιστούν στην Ενιαία Κρατική Εξέταση, αλλά έχουν ενδιαφέρον, μην τους χάσετε!
Αυτό είναι όλο! Καλή σου τύχη!
Με εκτίμηση, Alexander Krutitskikh
P.S: Θα σας ήμουν ευγνώμων αν μου πείτε για τον ιστότοπο στα κοινωνικά δίκτυα.
Σε αυτό το σεμινάριο βίντεο θα εξετάσουμε την επίλυση μιας αρκετά σοβαρής λογαριθμικής εξίσωσης, στην οποία όχι μόνο πρέπει να βρείτε τις ρίζες, αλλά και να επιλέξετε αυτές που βρίσκονται σε ένα δεδομένο τμήμα.
Πρόβλημα Γ1. Λύστε την εξίσωση. Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα.
Σημείωση για τις λογαριθμικές εξισώσεις
Ωστόσο, από χρόνο σε χρόνο έρχονται σε μένα φοιτητές που προσπαθούν να λύσουν τέτοια, ειλικρινά, δύσκολες εξισώσεις, αλλά ταυτόχρονα δεν μπορούν να καταλάβουν: από πού να ξεκινήσουν και πώς να προσεγγίσουν τους λογάριθμους; Αυτό το πρόβλημα μπορεί να προκύψει ακόμη και μεταξύ δυνατών, καλά προετοιμασμένων μαθητών.
Ως αποτέλεσμα, πολλοί αρχίζουν να φοβούνται αυτό το θέμα ή ακόμη και να θεωρούν τον εαυτό τους ανόητο. Λοιπόν, θυμηθείτε: αν δεν μπορείτε να λύσετε μια τέτοια εξίσωση, αυτό δεν σημαίνει καθόλου ότι είστε ανόητοι. Επειδή, για παράδειγμα, μπορείτε να χειριστείτε αυτήν την εξίσωση σχεδόν προφορικά:
ημερολόγιο 2 x = 4
Και αν δεν είναι έτσι, δεν θα διαβάζατε αυτό το κείμενο τώρα, γιατί ήσασταν απασχολημένοι με απλούστερες και πιο κοσμικές εργασίες. Φυσικά, κάποιος θα αντιταχθεί τώρα: «Τι σχέση έχει αυτή η απλούστερη εξίσωση με την υγιή δομή μας;» Απαντώ: οποιαδήποτε λογαριθμική εξίσωση, όσο περίπλοκη κι αν είναι, τελικά καταλήγει σε αυτές τις απλούστερες δομές που μπορούν να λυθούν προφορικά.
Φυσικά, πρέπει κανείς να μετακινηθεί από σύνθετες λογαριθμικές εξισώσεις σε απλούστερες όχι μέσω επιλογής ή χορού με ντέφι, αλλά σύμφωνα με σαφείς, μακροπρόθεσμους κανόνες, οι οποίοι ονομάζονται - κανόνες μετατροπής λογαριθμικών παραστάσεων. Γνωρίζοντας τα, μπορείτε εύκολα να αντιμετωπίσετε ακόμη και τις πιο περίπλοκες εξισώσεις στην Εξέταση Ενιαίου Κράτους στα μαθηματικά.
Και είναι αυτοί οι κανόνες για τους οποίους θα μιλήσουμε στο σημερινό μάθημα. Πηγαίνω!
Επίλυση της λογαριθμικής εξίσωσης στο πρόβλημα Γ1
Λοιπόν, ας λύσουμε την εξίσωση:
Πρώτα απ 'όλα, όταν πρόκειται για λογαριθμικές εξισώσεις, θυμόμαστε τις βασικές τακτικές - ας πούμε, τον βασικό κανόνα για την επίλυση λογαριθμικών εξισώσεων. Αποτελείται από τα εξής:
Το θεώρημα της κανονικής μορφής. Οποιαδήποτε λογαριθμική εξίσωση, ανεξάρτητα από το τι περιλαμβάνεται σε αυτήν, ανεξάρτητα από τους λογάριθμους, σε ποια βάση και ανεξάρτητα από το τι περιέχει, πρέπει απαραίτητα να αναχθεί σε μια εξίσωση της μορφής:
log a f (x) = log a g (x)
Αν κοιτάξουμε την εξίσωσή μας, παρατηρούμε αμέσως δύο προβλήματα:
- Αριστερά έχουμε άθροισμα δύο αριθμών, ένα από τα οποία δεν είναι καθόλου λογάριθμος.
- Στα δεξιά υπάρχει αρκετά λογάριθμος, αλλά στη βάση του υπάρχει μια ρίζα. Και ο λογάριθμος στα αριστερά είναι απλά 2, δηλ. Οι βάσεις των λογαρίθμων αριστερά και δεξιά είναι διαφορετικές.
Έτσι, συντάξαμε αυτήν τη λίστα προβλημάτων που διαχωρίζουν την εξίσωσή μας από αυτήν κανονική εξίσωση, στο οποίο πρέπει να ανάγεται οποιαδήποτε λογαριθμική εξίσωση κατά τη διαδικασία επίλυσης. Έτσι, η επίλυση της εξίσωσης σε αυτό το στάδιο καταλήγει στην εξάλειψη των δύο προβλημάτων που περιγράφηκαν παραπάνω.
Οποιαδήποτε λογαριθμική εξίσωση μπορεί να λυθεί γρήγορα και εύκολα αν την αναγάγετε στην κανονική της μορφή.
Άθροισμα λογαρίθμων και λογάριθμου γινομένου
Ας προχωρήσουμε με τη σειρά. Αρχικά, ας δούμε τη δομή στα αριστερά. Τι μπορούμε να πούμε για το άθροισμα δύο λογαρίθμων; Ας θυμηθούμε την υπέροχη φόρμουλα:
log a f (x) + log a g (x) = log a f (x) g (x)
Αξίζει όμως να λάβουμε υπόψη ότι στην περίπτωσή μας ο πρώτος όρος δεν είναι καθόλου λογάριθμος. Αυτό σημαίνει ότι πρέπει να αναπαραστήσουμε τη μονάδα ως λογάριθμο στη βάση 2 (ακριβώς 2, επειδή ο λογάριθμος στη βάση 2 είναι στα αριστερά). Πως να το κάνεις; Ας θυμηθούμε ξανά την υπέροχη φόρμουλα:
α = ημερολόγιο β β α
Εδώ πρέπει να καταλάβετε: όταν λέμε «Οποιαδήποτε βάση b», εννοούμε ότι το b εξακολουθεί να μην μπορεί να είναι αυθαίρετος αριθμός. Αν εισάγουμε έναν αριθμό σε έναν λογάριθμο, βέβαιο περιορισμούς, δηλαδή: η βάση του λογάριθμου πρέπει να είναι μεγαλύτερη από 0 και δεν πρέπει να είναι ίση με 1. Διαφορετικά, ο λογάριθμος απλά δεν έχει νόημα. Ας το γράψουμε αυτό:
0 < b ≠ 1
Ας δούμε τι συμβαίνει στην περίπτωσή μας:
1 = ημερολόγιο 2 2 1 = ημερολόγιο 2 2
Τώρα ας ξαναγράψουμε ολόκληρη την εξίσωσή μας λαμβάνοντας υπόψη αυτό το γεγονός. Και αμέσως εφαρμόζουμε έναν άλλο κανόνα: το άθροισμα των λογαρίθμων είναι ίσο με το λογάριθμο του γινόμενου των ορισμάτων. Ως αποτέλεσμα παίρνουμε:

Έχουμε μια νέα εξίσωση. Όπως βλέπουμε, είναι ήδη πολύ πιο κοντά στην κανονική εξίσωση που επιδιώκουμε. Αλλά υπάρχει ένα πρόβλημα, το καταγράψαμε ως δεύτερο σημείο: οι λογάριθμοί μας, που είναι αριστερά και δεξιά, διαφορετικούς λόγους. Ας προχωρήσουμε στο επόμενο βήμα.
Κανόνες αφαίρεσης δυνάμεων από τον λογάριθμο
Άρα ο λογάριθμος στα αριστερά έχει βάση μόλις 2 και ο λογάριθμος στα δεξιά έχει μια ρίζα στη βάση. Αλλά αυτό δεν είναι πρόβλημα εάν θυμηθούμε ότι οι βάσεις των ορισμάτων του λογαρίθμου μπορούν να ανυψωθούν σε δυνάμεις. Ας γράψουμε έναν από αυτούς τους κανόνες:
log a b n = n log a b
Μεταφρασμένο στην ανθρώπινη γλώσσα: μπορείτε να αφαιρέσετε τη δύναμη από τη βάση του λογάριθμου και να την βάλετε μπροστά ως πολλαπλασιαστή. Ο αριθμός n «μετανάστευσε» από τον λογάριθμο προς τα έξω και έγινε συντελεστής μπροστά.
Μπορούμε εξίσου εύκολα να αντλήσουμε την ισχύ από τη βάση του λογαρίθμου. Θα μοιάζει με αυτό:

Με άλλα λόγια, αν αφαιρέσετε τη μοίρα από το όρισμα του λογάριθμου, αυτός ο βαθμός γράφεται και ως παράγοντας πριν από τον λογάριθμο, αλλά όχι ως αριθμός, αλλά ως ο αντίστροφος αριθμός 1/k.
Ωστόσο, δεν είναι μόνο αυτό! Μπορούμε να συνδυάσουμε αυτούς τους δύο τύπους και να καταλήξουμε στον ακόλουθο τύπο:

Όταν μια ισχύς εμφανίζεται και στη βάση και στο όρισμα ενός λογαρίθμου, μπορούμε να εξοικονομήσουμε χρόνο και να απλοποιήσουμε τους υπολογισμούς αφαιρώντας αμέσως τις δυνάμεις τόσο από τη βάση όσο και από το όρισμα. Σε αυτήν την περίπτωση, αυτό που ήταν στο όρισμα (στην περίπτωσή μας, αυτός είναι ο συντελεστής n) θα εμφανιστεί στον αριθμητή. Και ποιος ήταν ο βαθμός στη βάση, ένα k, θα πάει στον παρονομαστή.
Και είναι αυτοί οι τύποι που θα χρησιμοποιήσουμε τώρα για να μειώσουμε τους λογάριθμους μας στην ίδια βάση.
Πρώτα από όλα, ας διαλέξουμε μια λίγο πολύ όμορφη βάση. Προφανώς, είναι πολύ πιο ευχάριστο να δουλεύεις με δύο στη βάση παρά με ρίζα. Ας προσπαθήσουμε λοιπόν να μειώσουμε τον δεύτερο λογάριθμο στη βάση 2. Ας γράψουμε αυτόν τον λογάριθμο ξεχωριστά:
![]()
Τι μπορούμε να κάνουμε εδώ; Ας θυμηθούμε τον τύπο ισχύος με λογικό εκθέτη. Με άλλα λόγια, μπορούμε να γράψουμε τις ρίζες ως δύναμη με λογικό εκθέτη. Και τότε παίρνουμε τη δύναμη του 1/2 τόσο από το όρισμα όσο και από τη βάση του λογαρίθμου. Μειώνουμε τα δύο στους συντελεστές στον αριθμητή και στον παρονομαστή που βλέπει στον λογάριθμο:

Τέλος, ας ξαναγράψουμε την αρχική εξίσωση λαμβάνοντας υπόψη τους νέους συντελεστές:
ημερολόγιο 2 2(9x 2 + 5) = ημερολόγιο 2 (8x 4 + 14)
Λάβαμε την κανονική λογαριθμική εξίσωση. Τόσο στα αριστερά όσο και στα δεξιά έχουμε λογάριθμο στην ίδια βάση 2. Εκτός από αυτούς τους λογάριθμους, δεν υπάρχουν συντελεστές, ούτε όροι ούτε στα αριστερά ούτε στα δεξιά.
Κατά συνέπεια, μπορούμε να απαλλαγούμε από το πρόσημο του λογαρίθμου. Φυσικά, λαμβάνοντας υπόψη το πεδίο ορισμού. Αλλά πριν το κάνουμε αυτό, ας επιστρέψουμε και ας κάνουμε μια μικρή διευκρίνιση σχετικά με τα κλάσματα.
Διαίρεση κλάσματος με κλάσμα: Πρόσθετες εκτιμήσεις
Δεν καταλαβαίνουν όλοι οι μαθητές από πού προέρχονται και πού πηγαίνουν οι παράγοντες μπροστά από τον σωστό λογάριθμο. Ας το ξαναγράψουμε:

Ας καταλάβουμε τι είναι ένα κλάσμα. Ας γράψουμε:
Τώρα ας θυμηθούμε τον κανόνα για τη διαίρεση των κλασμάτων: για να διαιρέσουμε με το 1/2 πρέπει να πολλαπλασιάσουμε με το ανεστραμμένο κλάσμα:

Φυσικά, για τη διευκόλυνση των περαιτέρω υπολογισμών, μπορούμε να γράψουμε δύο ως 2/1 - και αυτό είναι που παρατηρούμε ως ο δεύτερος συντελεστής στη διαδικασία επίλυσης.
Ελπίζω τώρα όλοι να καταλάβουν από πού προέρχεται ο δεύτερος συντελεστής, οπότε ας προχωρήσουμε απευθείας στην επίλυση της κανονικής λογαριθμικής μας εξίσωσης.
Απαλλαγείτε από το σύμβολο του λογάριθμου
Επιτρέψτε μου να σας υπενθυμίσω ότι τώρα μπορούμε να απαλλαγούμε από τους λογάριθμους και να αφήσουμε την ακόλουθη έκφραση:
2(9x 2 + 5) = 8x 4 + 14
Ας ανοίξουμε τις αγκύλες στα αριστερά. Παίρνουμε:
18x 2 + 10 = 8 x 4 + 14
Ας μετακινήσουμε τα πάντα από την αριστερή πλευρά προς τα δεξιά:
8x 4 + 14 − 18x 2 − 10 = 0
Ας φέρουμε παρόμοια και ας πάρουμε:
8x 4 − 18x 2 + 4 = 0
Μπορούμε να διαιρέσουμε και τις δύο πλευρές αυτής της εξίσωσης με 2 για να απλοποιήσουμε τους συντελεστές και παίρνουμε:
4x 4 − 9x 2 + 2 = 0
Μπροστά μας είναι το συνηθισμένο διτετραγωνική εξίσωση, και οι ρίζες του υπολογίζονται εύκολα μέσω της διάκρισης. Λοιπόν, ας γράψουμε τη διάκριση:
D = 81 − 4 4 2 = 81 − 32 = 49
Ωραία, το διακριτικό είναι «όμορφο», η ρίζα του είναι 7. Αυτό είναι όλο, ας μετρήσουμε το Χ εμείς οι ίδιοι. Αλλά σε αυτήν την περίπτωση, οι ρίζες δεν θα είναι x, αλλά x 2, επειδή έχουμε μια διτετραγωνική εξίσωση. Λοιπόν, οι επιλογές μας:
Παρακαλώ σημειώστε: εξαγάγαμε τις ρίζες, οπότε θα υπάρχουν δύο απαντήσεις, επειδή... τετράγωνο - ομοιόμορφη λειτουργία. Και αν γράψουμε μόνο τη ρίζα των δύο, τότε απλά θα χάσουμε τη δεύτερη ρίζα.
Τώρα γράφουμε τη δεύτερη ρίζα της διτετραγωνικής μας εξίσωσης:

Και πάλι, παίρνουμε την αριθμητική τετραγωνική ρίζα και των δύο πλευρών της εξίσωσής μας και παίρνουμε δύο ρίζες. Ωστόσο, να θυμάστε:
Δεν αρκεί απλώς να εξισώνουμε τα επιχειρήματα των λογαρίθμων σε κανονική μορφή. Θυμηθείτε τον τομέα του ορισμού!
Συνολικά πήραμε τέσσερις ρίζες. Όλα αυτά είναι πράγματι λύσεις στην αρχική μας εξίσωση. Ρίξτε μια ματιά: στην αρχική μας λογαριθμική εξίσωση, οι λογάριθμοι στο εσωτερικό είναι είτε 9x 2 + 5 (αυτή η συνάρτηση είναι πάντα θετική) είτε 8x 4 + 14 - που είναι επίσης πάντα θετικό. Επομένως, το πεδίο ορισμού των λογαρίθμων ικανοποιείται σε κάθε περίπτωση, όποια ρίζα κι αν πάρουμε, πράγμα που σημαίνει ότι και οι τέσσερις ρίζες είναι λύσεις της εξίσωσής μας.
Ωραία, τώρα ας περάσουμε στο δεύτερο μέρος του προβλήματος.
Επιλογή ριζών λογαριθμικής εξίσωσης σε τμήμα
Από τις τέσσερις ρίζες μας επιλέγουμε αυτές που βρίσκονται στο τμήμα [−1; 8/9]. Επιστρέφουμε στις ρίζες μας και τώρα θα πραγματοποιήσουμε την επιλογή τους. Αρχικά, προτείνω να σχεδιάσετε έναν άξονα συντεταγμένων και να σημειώσετε τα άκρα του τμήματος σε αυτόν:

Και τα δύο σημεία θα είναι σκιασμένα. Εκείνοι. Σύμφωνα με τις συνθήκες του προβλήματος, μας ενδιαφέρει το σκιασμένο τμήμα. Τώρα ας δούμε τις ρίζες.
Παράλογες ρίζες
Ας ξεκινήσουμε με παράλογες ρίζες. Σημειώστε ότι 8/9< 9/9 = 1. С другой стороны, корень из двух явно больше единицы. Следовательно, наши корни будут находиться на отрезке в таком положении:

Από αυτό προκύπτει ότι η ρίζα των δύο δεν εμπίπτει στο τμήμα που μας ενδιαφέρει. Ομοίως, θα λάβουμε με μια αρνητική ρίζα: είναι μικρότερη από −1, δηλαδή βρίσκεται στα αριστερά του τμήματος που μας ενδιαφέρει.
Ορθολογικές ρίζες
Απομένουν δύο ρίζες: x = 1/2 και x = −1/2. Ας παρατηρήσουμε ότι το αριστερό άκρο του τμήματος (−1) είναι αρνητικό και το δεξί άκρο (8/9) είναι θετικό. Επομένως, κάπου ανάμεσα σε αυτά τα άκρα βρίσκεται ο αριθμός 0. Η ρίζα x = −1/2 θα είναι μεταξύ −1 και 0, δηλ. θα καταλήξει στην τελική απάντηση. Κάνουμε το ίδιο με τη ρίζα x = 1/2. Αυτή η ρίζα βρίσκεται επίσης στο υπό εξέταση τμήμα.
Μπορείτε να βεβαιωθείτε ότι το 8/9 είναι μεγαλύτερο από το 1/2. Ας αφαιρέσουμε αυτούς τους αριθμούς ο ένας από τον άλλο:
Πήραμε το κλάσμα 7/18 > 0, που εξ ορισμού σημαίνει ότι 8/9 > 1/2.
Ας σημειώσουμε τις κατάλληλες ρίζες στον άξονα συντεταγμένων:
Η τελική απάντηση θα είναι δύο ρίζες: 1/2 και −1/2.
Σύγκριση παράλογων αριθμών: ένας καθολικός αλγόριθμος
Εν κατακλείδι, θα ήθελα να επιστρέψω για άλλη μια φορά στους παράλογους αριθμούς. Χρησιμοποιώντας το παράδειγμά τους, θα δούμε τώρα πώς να συγκρίνουμε ορθολογικά και παράλογα μεγέθη στα μαθηματικά. Κατ 'αρχάς, υπάρχει ένα τέτοιο τσιμπούρι μεταξύ τους V - ένα σημάδι "περισσότερο" ή "λιγότερο", αλλά δεν γνωρίζουμε ακόμη σε ποια κατεύθυνση κατευθύνεται. Ας γράψουμε:
Γιατί χρειαζόμαστε καθόλου αλγόριθμους σύγκρισης; Το γεγονός είναι ότι σε αυτό το πρόβλημα ήμασταν πολύ τυχεροί: στη διαδικασία επίλυσης του διαιρετικού αριθμού 1 προέκυψε, για το οποίο μπορούμε σίγουρα να πούμε:

Ωστόσο, δεν θα δείτε πάντα έναν τέτοιο αριθμό αμέσως. Ας προσπαθήσουμε λοιπόν να συγκρίνουμε τους αριθμούς μας κατά μέτωπο, άμεσα.
Πώς γίνεται; Κάνουμε το ίδιο όπως με τις συνηθισμένες ανισότητες:
- Πρώτον, αν κάπου είχαμε αρνητικούς συντελεστές, θα πολλαπλασιάζαμε και τις δύο πλευρές της ανισότητας επί −1. Φυσικά αλλάζοντας την πινακίδα. Αυτό το σημάδι ελέγχου V θα άλλαζε σε αυτό - Λ.
- Αλλά στην περίπτωσή μας, και οι δύο πλευρές είναι ήδη θετικές, επομένως δεν χρειάζεται να αλλάξουμε τίποτα. Αυτό που πραγματικά χρειάζεται είναι τετράγωνο και τις δύο πλευρέςγια να απαλλαγούμε από το ριζοσπάστη.
Εάν, κατά τη σύγκριση των παράλογων αριθμών, δεν είναι δυνατή η άμεση επιλογή του διαχωριστικού στοιχείου, συνιστώ να εκτελέσετε μια τέτοια σύγκριση "κατά μέτωπο" - περιγράφοντάς την ως μια συνηθισμένη ανισότητα.
Κατά την επίλυσή του, επισημοποιείται ως εξής:

Τώρα είναι εύκολο να συγκριθούν όλα. Το θέμα είναι ότι 64/81< 81/81 = 1 < 2. На основании той цепочки преобразований мы заключаем, что 64/81 < 2 и, следовательно, корень больше 8/9.
Αυτό ήταν, έχουμε λάβει αυστηρή απόδειξη ότι όλοι οι αριθμοί σημειώνονται στην αριθμητική γραμμή x σωστά και ακριβώς με τη σειρά με την οποία θα έπρεπε να είναι στην πραγματικότητα. Κανείς δεν θα βρει σφάλμα με αυτή τη λύση, γι' αυτό θυμηθείτε: αν δεν δείτε αμέσως τον αριθμό διαίρεσης (στην περίπτωσή μας είναι 1), τότε μη διστάσετε να γράψετε την παραπάνω κατασκευή, να την πολλαπλασιάσετε, να την τετραγωνίσετε - και στο τέλος θα αποκτήσετε μια όμορφη ανισότητα. Από αυτή την ανισότητα θα φανεί ποιος αριθμός είναι μεγαλύτερος και ποιος μικρότερος.
Επιστρέφοντας στο πρόβλημά μας, θα ήθελα για άλλη μια φορά να επιστήσω την προσοχή σας σε αυτό που κάναμε στην αρχή όταν λύναμε την εξίσωσή μας. Δηλαδή: ρίξαμε μια προσεκτική ματιά στην αρχική μας λογαριθμική εξίσωση και προσπαθήσαμε να τη μειώσουμε σε κανονικόςλογαριθμική εξίσωση. Όπου υπάρχουν μόνο λογάριθμοι αριστερά και δεξιά - χωρίς επιπλέον όρους, συντελεστές μπροστά κ.λπ. Δεν χρειαζόμαστε δύο λογάριθμους με βάση το a ή το b, αλλά έναν λογάριθμο ίσο με έναν άλλο λογάριθμο.
Επιπλέον, οι βάσεις των λογαρίθμων πρέπει επίσης να είναι ίσες. Επιπλέον, εάν η εξίσωση συντίθεται σωστά, τότε με τη βοήθεια στοιχειωδών λογαριθμικών μετασχηματισμών (άθροισμα λογαρίθμων, μετατροπή αριθμού σε λογάριθμο κ.λπ.) θα ανάγουμε αυτή την εξίσωση στην κανονική.
Επομένως, από τώρα και στο εξής, όταν βλέπετε μια λογαριθμική εξίσωση που δεν μπορεί να λυθεί αμέσως, δεν πρέπει να χαθείτε ή να προσπαθήσετε να βρείτε την απάντηση. Το μόνο που χρειάζεται να κάνετε είναι να ακολουθήσετε αυτά τα βήματα:
- Μετατροπή όλων των ελεύθερων στοιχείων σε λογάριθμο.
- Στη συνέχεια, προσθέστε αυτούς τους λογάριθμους.
- Στην κατασκευή που προκύπτει, όλοι οι λογάριθμοι ανάγονται στην ίδια βάση.
Ως αποτέλεσμα, θα λάβετε μια απλή εξίσωση που μπορεί να λυθεί χρησιμοποιώντας στοιχειώδη εργαλεία άλγεβρας από υλικά τάξης 8-9. Γενικά, πηγαίνετε στον ιστότοπό μου, εξασκηθείτε στην επίλυση λογαρίθμων, λύστε λογαριθμικές εξισώσεις όπως εγώ, λύστε τις καλύτερα από εμένα. Και αυτό είναι όλο για μένα. Ο Πάβελ Μπέρντοφ ήταν μαζί σου. Τα λέμε!
Λογαριθμικές εξισώσεις. Συνεχίζουμε να εξετάζουμε προβλήματα από το Μέρος Β της Ενιαίας Κρατικής Εξέτασης στα μαθηματικά. Έχουμε ήδη εξετάσει λύσεις σε ορισμένες εξισώσεις στα άρθρα "", "". Σε αυτό το άρθρο θα δούμε τις λογαριθμικές εξισώσεις. Θα πω αμέσως ότι δεν θα υπάρξουν περίπλοκοι μετασχηματισμοί κατά την επίλυση τέτοιων εξισώσεων στην Ενιαία Κρατική Εξέταση. Είναι απλοί.
Αρκεί να γνωρίζουμε και να κατανοούμε τη βασική λογαριθμική ταυτότητα, να γνωρίζουμε τις ιδιότητες του λογαρίθμου. Σημειώστε ότι αφού το λύσετε, ΠΡΕΠΕΙ να κάνετε έναν έλεγχο - να αντικαταστήσετε την προκύπτουσα τιμή στην αρχική εξίσωση και να υπολογίσετε, στο τέλος θα πρέπει να πάρετε τη σωστή ισότητα.
Ορισμός:
Ο λογάριθμος ενός αριθμού στη βάση b είναι ο εκθέτης,στο οποίο πρέπει να ανυψωθεί το b για να ληφθεί το α.


Για παράδειγμα:
Log 3 9 = 2, αφού 3 2 = 9
Ιδιότητες λογαρίθμων:

Ειδικές περιπτώσεις λογαρίθμων:

Ας λύσουμε προβλήματα. Στο πρώτο παράδειγμα θα κάνουμε έναν έλεγχο. Κάντε μόνοι σας τον επόμενο έλεγχο.
Βρείτε τη ρίζα της εξίσωσης: log 3 (4–x) = 4
Αφού log b a = x b x = a, τότε
3 4 = 4 – x
x = 4 – 81
x = – 77
Εξέταση:
ημερολόγιο 3 (4–(–77)) = 4
ημερολόγιο 3 81 = 4
3 4 = 81 Σωστό.
Απάντηση: – 77
Αποφασίστε μόνοι σας:
Βρείτε τη ρίζα της εξίσωσης: log 2 (4 – x) = 7
Βρείτε τη ρίζα του ημερολογίου εξίσωσης 5(4 + x) = 2
Χρησιμοποιούμε τη βασική λογαριθμική ταυτότητα.
Αφού log a b = x b x = a, τότε
5 2 = 4 + x
x =5 2 – 4
x = 21
Εξέταση:
ημερολόγιο 5 (4 + 21) = 2
ημερολόγιο 5 25 = 2
5 2 = 25 Σωστό.
Απάντηση: 21
Βρείτε τη ρίζα της εξίσωσης log 3 (14 – x) = log 3 5.
Η ακόλουθη ιδιότητα λαμβάνει χώρα, η σημασία της είναι η εξής: αν στην αριστερή και δεξιά πλευρά της εξίσωσης έχουμε λογάριθμους με την ίδια βάση, τότε μπορούμε να εξισώσουμε τις εκφράσεις κάτω από τα πρόσημα των λογαρίθμων.
14 – x = 5
x=9
Κάντε έναν έλεγχο.
Απάντηση: 9
Αποφασίστε μόνοι σας:
Βρείτε τη ρίζα της εξίσωσης log 5 (5 – x) = log 5 3.
Βρείτε τη ρίζα της εξίσωσης: log 4 (x + 3) = log 4 (4x – 15).
Αν log c a = log c b, τότε a = b
x + 3 = 4x – 15
3x = 18
x = 6
Κάντε έναν έλεγχο.
Απάντηση: 6
Βρείτε τη ρίζα της εξίσωσης log 1/8 (13 – x) = – 2.
(1/8) –2 = 13 – x
8 2 = 13 – x
x = 13 – 64
x = – 51
Κάντε έναν έλεγχο.
Μια μικρή προσθήκη - το ακίνητο χρησιμοποιείται εδώ
βαθμούς ().
Απάντηση: – 51
Αποφασίστε μόνοι σας:
Βρείτε τη ρίζα της εξίσωσης: log 1/7 (7 – x) = – 2
Βρείτε τη ρίζα της εξίσωσης log 2 (4 – x) = 2 log 2 5.
Ας μεταμορφώσουμε τη δεξιά πλευρά. Ας χρησιμοποιήσουμε το ακίνητο:
log a b m = m∙log a b
log 2 (4 – x) = log 2 5 2
Αν log c a = log c b, τότε a = b
4 – x = 5 2
4 – x = 25
x = – 21
Κάντε έναν έλεγχο.
Απάντηση: – 21
Αποφασίστε μόνοι σας:
Βρείτε τη ρίζα της εξίσωσης: log 5 (5 – x) = 2 log 5 3
Λύστε την εξίσωση log 5 (x 2 + 4x) = log 5 (x 2 + 11)
Αν log c a = log c b, τότε a = b
x 2 + 4x = x 2 + 11
4x = 11
x = 2,75
Κάντε έναν έλεγχο.
Απάντηση: 2,75
Αποφασίστε μόνοι σας:
Βρείτε τη ρίζα της εξίσωσης log 5 (x 2 + x) = log 5 (x 2 + 10).
Λύστε την εξίσωση log 2 (2 – x) = log 2 (2 – 3x) +1.
Είναι απαραίτητο να λάβουμε μια έκφραση της φόρμας στη δεξιά πλευρά της εξίσωσης:
ημερολόγιο 2 (......)
Αντιπροσωπεύουμε το 1 ως λογάριθμο βάσης 2:
1 = ημερολόγιο 2 2
log c (ab) = log c a + log c b
log 2 (2 – x) = log 2 (2 – 3x) + log 2 2
Παίρνουμε:
log 2 (2 – x) = log 2 2 (2 – 3x)
Αν log c a = log c b, τότε a = b, τότε
2 – x = 4 – 6x
5x = 2
x = 0,4
Κάντε έναν έλεγχο.
Απάντηση: 0,4
Αποφασίστε μόνοι σας: Στη συνέχεια πρέπει να λύσετε την τετραγωνική εξίσωση. Παρεμπιπτόντως,
οι ρίζες είναι 6 και – 4.
Ρίζα "-Το 4" δεν είναι λύση, αφού η βάση του λογαρίθμου πρέπει να είναι μεγαλύτερη από το μηδέν και με "– 4" ισούται με " – 5". Η λύση είναι η ρίζα 6.Κάντε έναν έλεγχο.
Απάντηση: 6.
R φάτε μόνοι σας:
Λύστε την εξίσωση log x –5 49 = 2. Αν η εξίσωση έχει περισσότερες από μία ρίζες, απαντήστε με τη μικρότερη.
Όπως είδατε, δεν υπάρχουν περίπλοκοι μετασχηματισμοί με λογαριθμικές εξισώσειςΟχι. Αρκεί να γνωρίζουμε τις ιδιότητες του λογάριθμου και να μπορούμε να τις εφαρμόζουμε. Σε προβλήματα USE που σχετίζονται με τον μετασχηματισμό λογαριθμικών παραστάσεων, εκτελούνται πιο σοβαροί μετασχηματισμοί και απαιτούνται πιο εις βάθος δεξιότητες επίλυσης. Θα δούμε τέτοια παραδείγματα, μην τα χάσετε!Σου εύχομαι επιτυχία!!!
Με εκτίμηση, Alexander Krutitskikh.
P.S: Θα σας ήμουν ευγνώμων αν μου πείτε για τον ιστότοπο στα κοινωνικά δίκτυα.
- Σε επαφή με 0
- Google+ 0
- Εντάξει 0
- Facebook 0