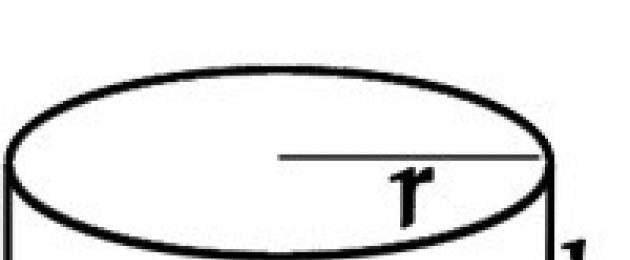
Ο κύλινδρος είναι ένα γεωμετρικό σώμα που οριοθετείται από δύο παράλληλα επίπεδα και μια κυλινδρική επιφάνεια. Στο άρθρο, θα μιλήσουμε για το πώς να βρούμε την περιοχή ενός κυλίνδρου και, χρησιμοποιώντας τον τύπο, θα λύσουμε πολλά προβλήματα για παράδειγμα.
Ένας κύλινδρος έχει τρεις επιφάνειες: μια πάνω, μια κάτω και μια πλευρική επιφάνεια.
Το πάνω και το κάτω μέρος του κυλίνδρου είναι κύκλοι και είναι εύκολο να αναγνωριστούν.
Είναι γνωστό ότι το εμβαδόν ενός κύκλου είναι ίσο με πr 2. Επομένως, ο τύπος για την περιοχή δύο κύκλων (πάνω και κάτω μέρος του κυλίνδρου) θα μοιάζει με πr 2 + πr 2 = 2πr 2 .
Η τρίτη, πλευρική επιφάνεια του κυλίνδρου, είναι το καμπύλο τοίχωμα του κυλίνδρου. Για να αναπαραστήσουμε καλύτερα αυτή την επιφάνεια, ας προσπαθήσουμε να την μεταμορφώσουμε ώστε να αποκτήσει ένα αναγνωρίσιμο σχήμα. Φανταστείτε ότι ένας κύλινδρος είναι ένα συνηθισμένο κουτί από κασσίτερο που δεν έχει επάνω καπάκι και κάτω. Ας κάνουμε μια κατακόρυφη τομή στο πλευρικό τοίχωμα από την κορυφή προς το κάτω μέρος του βάζου (Βήμα 1 στο σχήμα) και ας προσπαθήσουμε να ανοίξουμε (ισιώσει) όσο το δυνατόν περισσότερο το σχήμα που προκύπτει (Βήμα 2).
Μετά την πλήρη αποκάλυψη του προκύπτοντος βάζου, θα δούμε μια γνωστή φιγούρα (Βήμα 3), αυτό είναι ένα ορθογώνιο. Το εμβαδόν ενός ορθογωνίου είναι εύκολο να υπολογιστεί. Αλλά πριν από αυτό, ας επιστρέψουμε για λίγο στον αρχικό κύλινδρο. Η κορυφή του αρχικού κυλίνδρου είναι ένας κύκλος και γνωρίζουμε ότι η περιφέρεια ενός κύκλου υπολογίζεται με τον τύπο: L = 2πr. Σημειώνεται με κόκκινο χρώμα στο σχήμα.
Όταν το πλευρικό τοίχωμα του κυλίνδρου διασταλεί πλήρως, βλέπουμε ότι η περιφέρεια γίνεται το μήκος του παραλληλογράμμου που προκύπτει. Οι πλευρές αυτού του ορθογωνίου θα είναι η περιφέρεια (L = 2πr) και το ύψος του κυλίνδρου (h). Το εμβαδόν ενός ορθογωνίου είναι ίσο με το γινόμενο των πλευρών του - S = μήκος x πλάτος = L x h = 2πr x h = 2πrh. Ως αποτέλεσμα, έχουμε αποκτήσει έναν τύπο για τον υπολογισμό της πλευρικής επιφάνειας ενός κυλίνδρου.
Ο τύπος για το εμβαδόν της πλευρικής επιφάνειας ενός κυλίνδρου
S πλευρά = 2 πρω
Πλήρης επιφάνεια ενός κυλίνδρου
Τέλος, αν αθροίσουμε το εμβαδόν και των τριών επιφανειών, παίρνουμε τον τύπο για τη συνολική επιφάνεια ενός κυλίνδρου. Η επιφάνεια του κυλίνδρου είναι ίση με την περιοχή της κορυφής του κυλίνδρου + την περιοχή της βάσης του κυλίνδρου + την περιοχή της πλευρικής επιφάνειας του κυλίνδρου ή S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Μερικές φορές αυτή η έκφραση γράφεται με τον ίδιο τύπο 2πr (r + h).
Ο τύπος για τη συνολική επιφάνεια ενός κυλίνδρου
S = 2πr 2 + 2πrh = 2πr(r + h)
r είναι η ακτίνα του κυλίνδρου, h είναι το ύψος του κυλίνδρου
Παραδείγματα υπολογισμού της επιφάνειας ενός κυλίνδρου
Για να κατανοήσουμε τους παραπάνω τύπους, ας προσπαθήσουμε να υπολογίσουμε την επιφάνεια ενός κυλίνδρου χρησιμοποιώντας παραδείγματα.
1. Η ακτίνα της βάσης του κυλίνδρου είναι 2, το ύψος είναι 3. Προσδιορίστε το εμβαδόν της πλευρικής επιφάνειας του κυλίνδρου.
Η συνολική επιφάνεια υπολογίζεται με τον τύπο: πλευρά S. = 2 πρω
S πλευρά = 2 * 3,14 * 2 * 34,6 . Συνολικές βαθμολογίες που ελήφθησαν: 990.
Σε αυτό το μάθημα:
- Εργασία 1. Βρείτε τη συνολική επιφάνεια της πυραμίδας
- Εργασία 2. Βρείτε το εμβαδόν της πλευρικής επιφάνειας μιας κανονικής τριγωνικής πυραμίδας
.
Σημείωση . Εάν πρέπει να λύσετε ένα πρόβλημα στη γεωμετρία, το οποίο δεν είναι εδώ - γράψτε για αυτό στο φόρουμ. Στις εργασίες, αντί για το σύμβολο "τετραγωνική ρίζα", χρησιμοποιείται η συνάρτηση sqrt (), στην οποία sqrt είναι το σύμβολο της τετραγωνικής ρίζας και η ριζική έκφραση υποδεικνύεται σε αγκύλες. Για απλές ριζικές εκφράσεις, μπορεί να χρησιμοποιηθεί το σύμβολο "√"..
Εργασία 1. Βρείτε τη συνολική επιφάνεια μιας κανονικής πυραμίδας
Το ύψος της βάσης μιας κανονικής τριγωνικής πυραμίδας είναι 3 cm και η γωνία μεταξύ της πλευρικής όψης και της βάσης της πυραμίδας είναι 45 μοίρες.Βρείτε τη συνολική επιφάνεια της πυραμίδας
Λύση.
Στη βάση μιας κανονικής τριγωνικής πυραμίδας βρίσκεται ένα ισόπλευρο τρίγωνο.
Επομένως, για να λύσουμε το πρόβλημα, χρησιμοποιούμε τις ιδιότητες ενός κανονικού τριγώνου: 
Γνωρίζουμε το ύψος του τριγώνου, από όπου μπορούμε να βρούμε το εμβαδόν του.
h = √3/2a
a = h / (√3/2)
a = 3 / (√3/2)
a = 6 / √3
Από όπου το εμβαδόν της βάσης θα είναι ίσο με:
S = √3/4 a 2
S = √3/4 (6 / √3) 2
S = 3√3
Για να βρούμε το εμβαδόν της πλευρικής όψης, υπολογίζουμε το ύψος KM. Η γωνία OKM, σύμφωνα με τη δήλωση προβλήματος, είναι 45 μοίρες.
Ετσι:
OK / MK = cos 45
Ας χρησιμοποιήσουμε τον πίνακα τιμών των τριγωνομετρικών συναρτήσεων και ας αντικαταστήσουμε τις γνωστές τιμές.
OK / MK = √2/2
Λαμβάνουμε υπόψη ότι το ΟΚ ισούται με την ακτίνα του εγγεγραμμένου κύκλου. Επειτα
ΟΚ = √3/6 α
ΟΚ = √3/6 * 6/√3 = 1
Επειτα
OK / MK = √2/2
1 / MK = √2/2
MK = 2/√2
Το εμβαδόν της πλευρικής όψης είναι τότε ίσο με το μισό γινόμενο του ύψους και της βάσης του τριγώνου.
Πλευρά = 1/2 (6 / √3) (2/√2) = 6/√6
Έτσι, η συνολική επιφάνεια της πυραμίδας θα είναι ίση με
S = 3√3 + 3 * 6/√6
S = 3√3 + 18/√6
Απάντηση: 3√3 + 18/√6
Εργασία 2. Βρείτε την πλευρική επιφάνεια μιας κανονικής πυραμίδας
Σε μια κανονική τριγωνική πυραμίδα, το ύψος είναι 10 cm και η πλευρά της βάσης είναι 16 cm . Βρείτε το εμβαδόν της πλευρικής επιφάνειας .Λύση.
Δεδομένου ότι η βάση μιας κανονικής τριγωνικής πυραμίδας είναι ένα ισόπλευρο τρίγωνο, τότε το AO είναι η ακτίνα του περιγεγραμμένου κύκλου γύρω από τη βάση.
(Απάγεται από)
Η ακτίνα ενός κύκλου που περιβάλλεται γύρω από ένα ισόπλευρο τρίγωνο βρίσκεται από τις ιδιότητές του
Οπότε το μήκος των άκρων μιας κανονικής τριγωνικής πυραμίδας θα είναι ίσο με:
AM 2 = MO 2 + AO 2
το ύψος της πυραμίδας είναι γνωστό από την συνθήκη (10 cm), AO = 16√3/3
AM 2 = 100 + 256/3
ΠΜ = √(556/3)
Κάθε πλευρά της πυραμίδας είναι ένα ισοσκελές τρίγωνο. Το εμβαδόν ενός ισοσκελούς τριγώνου βρίσκεται από τον πρώτο τύπο παρακάτω 
S = 1/2 * 16 sqrt((√(556/3) + 8) (√(556/3) - 8))
S = 8 sqrt((556/3) - 64)
S = 8 sqrt (364/3)
S = 16 sqrt (91/3)
Εφόσον και οι τρεις όψεις μιας κανονικής πυραμίδας είναι ίσες, η πλευρική επιφάνεια θα είναι ίση με
3S = 48√(91/3)
Απάντηση: 48 √(91/3)
Εργασία 3. Βρείτε τη συνολική επιφάνεια μιας κανονικής πυραμίδας
Η πλευρά μιας κανονικής τριγωνικής πυραμίδας είναι 3 cm και η γωνία μεταξύ της πλευρικής όψης και της βάσης της πυραμίδας είναι 45 μοίρες. Βρείτε τη συνολική επιφάνεια της πυραμίδας.
Λύση.
Δεδομένου ότι η πυραμίδα είναι κανονική, έχει ένα ισόπλευρο τρίγωνο στη βάση της. Άρα το εμβαδόν της βάσης είναι 
Άρα = 9 * √3/4
Για να βρούμε το εμβαδόν της πλευρικής όψης, υπολογίζουμε το ύψος KM. Η γωνία OKM, σύμφωνα με τη δήλωση προβλήματος, είναι 45 μοίρες.
Ετσι:
OK / MK = cos 45
Ας χρησιμοποιήσουμε
Τυπικά γεωμετρικά προβλήματα στο επίπεδο και στον τρισδιάστατο χώρο είναι τα προβλήματα προσδιορισμού των επιφανειών διαφορετικών σχημάτων. Σε αυτό το άρθρο, παρουσιάζουμε τον τύπο για το εμβαδόν της πλευρικής επιφάνειας μιας κανονικής τετραγωνικής πυραμίδας.
Τι είναι μια πυραμίδα;
Ας δώσουμε έναν αυστηρό γεωμετρικό ορισμό της πυραμίδας. Ας υποθέσουμε ότι υπάρχει κάποιο πολύγωνο με n πλευρές και n γωνίες. Επιλέγουμε ένα αυθαίρετο σημείο στο χώρο που δεν θα βρίσκεται στο επίπεδο του καθορισμένου n-γώνου και το συνδέουμε σε κάθε κορυφή του πολυγώνου. Θα πάρουμε ένα σχήμα που έχει κάποιο όγκο, το οποίο ονομάζεται n-γωνική πυραμίδα. Για παράδειγμα, ας δείξουμε στο παρακάτω σχήμα πώς μοιάζει μια πενταγωνική πυραμίδα.
Δύο σημαντικά στοιχεία οποιασδήποτε πυραμίδας είναι η βάση της (n-gon) και η κορυφή της. Αυτά τα στοιχεία συνδέονται μεταξύ τους με n τρίγωνα, τα οποία γενικά δεν είναι ίσα μεταξύ τους. Η κάθετη που πέφτει από την κορυφή στη βάση ονομάζεται ύψος του σχήματος. Αν τέμνει τη βάση στο γεωμετρικό κέντρο (συμπίπτει με το κέντρο μάζας του πολυγώνου), τότε μια τέτοια πυραμίδα ονομάζεται ευθεία γραμμή. Εάν, εκτός από αυτήν την συνθήκη, η βάση είναι ένα κανονικό πολύγωνο, τότε ολόκληρη η πυραμίδα ονομάζεται κανονική. Το παρακάτω σχήμα δείχνει πώς μοιάζουν οι κανονικές πυραμίδες με τριγωνικές, τετράγωνες, πενταγωνικές και εξαγωνικές βάσεις.
Η επιφάνεια της πυραμίδας
Πριν στραφούμε στο ζήτημα της περιοχής της πλευρικής επιφάνειας μιας κανονικής τετραγωνικής πυραμίδας, θα πρέπει να σταθούμε λεπτομερέστερα στην έννοια της ίδιας της επιφάνειας.
Όπως αναφέρθηκε παραπάνω και φαίνεται στα σχήματα, οποιαδήποτε πυραμίδα σχηματίζεται από ένα σύνολο όψεων ή πλευρών. Η μία πλευρά είναι η βάση και οι n πλευρές είναι τρίγωνα. Η επιφάνεια ολόκληρου του σχήματος είναι το άθροισμα των εμβαδών κάθε πλευράς του.
Είναι βολικό να μελετήσετε την επιφάνεια χρησιμοποιώντας το παράδειγμα μιας φιγούρας που ξεδιπλώνεται. Μια σάρωση για μια κανονική τετραγωνική πυραμίδα φαίνεται στα παρακάτω σχήματα.
Βλέπουμε ότι το εμβαδόν της επιφάνειάς του ισούται με το άθροισμα τεσσάρων εμβαδών πανομοιότυπων ισοσκελές τριγώνων και το εμβαδόν ενός τετραγώνου.
Το συνολικό εμβαδόν όλων των τριγώνων που σχηματίζουν τις πλευρές του σχήματος ονομάζεται εμβαδόν της πλευρικής επιφάνειας. Στη συνέχεια, δείχνουμε πώς να το υπολογίσουμε για μια κανονική τετραγωνική πυραμίδα.
Πλευρική επιφάνεια μιας ορθογώνιας κανονικής πυραμίδας
Για να υπολογίσουμε την πλευρική επιφάνεια του καθορισμένου σχήματος, στρέφουμε και πάλι στην παραπάνω σάρωση. Ας υποθέσουμε ότι γνωρίζουμε την πλευρά της τετραγωνικής βάσης. Ας το συμβολίσουμε με το σύμβολο α. Μπορεί να φανεί ότι καθένα από τα τέσσερα ίδια τρίγωνα έχει μια βάση μήκους a. Για να υπολογίσετε το συνολικό εμβαδόν τους, πρέπει να γνωρίζετε αυτή την τιμή για ένα τρίγωνο. Από την πορεία της γεωμετρίας είναι γνωστό ότι το εμβαδόν του τριγώνου S t είναι ίσο με το γινόμενο της βάσης και του ύψους, το οποίο πρέπει να διαιρεθεί στο μισό. Αυτό είναι:
Όπου h b είναι το ύψος του ισοσκελούς τριγώνου που σύρεται στη βάση α. Για μια πυραμίδα, αυτό το ύψος είναι το απόθεμα. Τώρα μένει να πολλαπλασιάσουμε την προκύπτουσα έκφραση με 4 για να πάρουμε την περιοχή S b της πλευρικής επιφάνειας για την εν λόγω πυραμίδα:
S b = 4*S t = 2*h b *a.
Αυτός ο τύπος περιέχει δύο παραμέτρους: το απόθεμα και την πλευρά της βάσης. Εάν το τελευταίο είναι γνωστό στις περισσότερες συνθήκες των προβλημάτων, τότε το πρώτο πρέπει να υπολογιστεί γνωρίζοντας άλλες ποσότητες. Ακολουθούν οι τύποι για τον υπολογισμό του αποθέματος h b για δύο περιπτώσεις:
- όταν είναι γνωστό το μήκος της πλευρικής πλευράς.
- όταν είναι γνωστό το ύψος της πυραμίδας.
Αν υποδηλώσουμε το μήκος της πλευρικής ακμής (την πλευρά ενός ισοσκελούς τριγώνου) με το σύμβολο L, τότε το απόθεμα h b καθορίζεται από τον τύπο:
h b \u003d √ (L 2 - a 2 / 4).
Αυτή η έκφραση είναι το αποτέλεσμα της εφαρμογής του Πυθαγόρειου θεωρήματος για το τρίγωνο της πλευρικής επιφάνειας.
Εάν το ύψος h της πυραμίδας είναι γνωστό, τότε το απότεμα h b μπορεί να υπολογιστεί ως εξής:
h b = √(h 2 + a 2 /4).
Δεν είναι επίσης δύσκολο να λάβουμε αυτήν την έκφραση εάν λάβουμε υπόψη ένα ορθογώνιο τρίγωνο μέσα στην πυραμίδα που σχηματίζεται από τα σκέλη h και a / 2 και την υποτείνουσα h b.
Θα δείξουμε πώς να εφαρμόσουμε αυτούς τους τύπους λύνοντας δύο ενδιαφέροντα προβλήματα.
Πρόβλημα με Γνωστή Επιφάνεια
Είναι γνωστό ότι το εμβαδόν της πλευρικής επιφάνειας ενός τετραγωνικού είναι 108 cm 2. Είναι απαραίτητο να υπολογιστεί η τιμή του μήκους του αποθέματός της h bif το ύψος της πυραμίδας είναι 7 cm.
Γράφουμε τον τύπο για το εμβαδόν S b της πλευρικής επιφάνειας μέσω του ύψους. Εχουμε:
S b = 2*√(h 2 + a 2 /4) *a.
Εδώ έχουμε απλώς αντικαταστήσει τον αντίστοιχο τύπο αποθέματος στην έκφραση για το S b . Ας τετραγωνίσουμε και τις δύο πλευρές της εξίσωσης:
S b 2 \u003d 4 * a 2 * h 2 + a 4.
Για να βρούμε την τιμή του a, κάνουμε μια αλλαγή μεταβλητών:
t 2 + 4*h 2 *t - S b 2 = 0.
Αντικαθιστούμε τώρα τις γνωστές τιμές και λύνουμε την τετραγωνική εξίσωση:
t 2 + 196*t - 11664 = 0.
Έχουμε γράψει μόνο τη θετική ρίζα αυτής της εξίσωσης. Τότε οι πλευρές της βάσης της πυραμίδας θα είναι ίσες με:
a = √t = √47,8355 ≈ 6,916 cm.
Για να λάβετε το μήκος του apotema, απλώς χρησιμοποιήστε τον τύπο:
h b \u003d √ (h 2 + a 2 / 4) \u003d √ (7 2 + 6,916 2 / 4) ≈ 7,808 cm.
Πλευρική επιφάνεια της πυραμίδας του Χέοπα
Ας προσδιορίσουμε την αξία της πλευράς για τη μεγαλύτερη αιγυπτιακή πυραμίδα. Είναι γνωστό ότι στη βάση του βρίσκεται ένα τετράγωνο με μήκος πλευράς 230.363 μέτρα. Το ύψος της κατασκευής ήταν αρχικά 146,5 μέτρα. Αντικαταστήστε αυτούς τους αριθμούς στον αντίστοιχο τύπο για το S b , παίρνουμε:
S b \u003d 2 * √ (h 2 + a 2 / 4) * a \u003d 2 * √ (146,5 2 + 230,363 2 / 4) * 230,363 ≈ 85860 m 2.
Η τιμή που βρέθηκε είναι ελαφρώς μεγαλύτερη από την περιοχή των 17 γηπέδων ποδοσφαίρου.
Ορισμός. Προφίλ- αυτό είναι ένα τρίγωνο στο οποίο η μία γωνία βρίσκεται στην κορυφή της πυραμίδας και η αντίθετη πλευρά της συμπίπτει με την πλευρά της βάσης (πολύγωνο).
Ορισμός. Πλαϊνά πλευράείναι οι κοινές πλευρές των πλευρικών όψεων. Μια πυραμίδα έχει τόσες άκρες όσες υπάρχουν γωνίες σε ένα πολύγωνο.
Ορισμός. ύψος πυραμίδαςείναι μια κάθετη που πέφτει από την κορυφή στη βάση της πυραμίδας.
Ορισμός. Απόθεμ- αυτή είναι η κάθετη της πλευρικής όψης της πυραμίδας, χαμηλωμένη από την κορυφή της πυραμίδας προς την πλευρά της βάσης.
Ορισμός. Διαγώνιο τμήμα- αυτό είναι ένα τμήμα της πυραμίδας από ένα επίπεδο που διέρχεται από την κορυφή της πυραμίδας και τη διαγώνιο της βάσης.
Ορισμός. Σωστή πυραμίδα- Αυτή είναι μια πυραμίδα στην οποία η βάση είναι ένα κανονικό πολύγωνο και το ύψος κατεβαίνει στο κέντρο της βάσης.
Όγκος και επιφάνεια της πυραμίδας
Τύπος. όγκος πυραμίδαςμέσω του εμβαδού και του ύψους της βάσης:
ιδιότητες πυραμίδας
Εάν όλες οι πλευρικές ακμές είναι ίσες, τότε ένας κύκλος μπορεί να περιγραφεί γύρω από τη βάση της πυραμίδας και το κέντρο της βάσης συμπίπτει με το κέντρο του κύκλου. Επίσης, η κάθετη που πέφτει από την κορυφή περνάει από το κέντρο της βάσης (κύκλος).
Εάν όλες οι πλευρικές νευρώσεις είναι ίσες, τότε έχουν κλίση προς το επίπεδο βάσης με τις ίδιες γωνίες.
Οι πλευρικές νευρώσεις είναι ίσες όταν σχηματίζουν ίσες γωνίες με το επίπεδο βάσης ή αν μπορεί να περιγραφεί ένας κύκλος γύρω από τη βάση της πυραμίδας.
Εάν οι πλευρικές όψεις είναι κεκλιμένες προς το επίπεδο της βάσης σε μία γωνία, τότε μπορεί να εγγραφεί ένας κύκλος στη βάση της πυραμίδας και η κορυφή της πυραμίδας να προβάλλεται στο κέντρο της.
Εάν οι πλευρικές όψεις είναι κεκλιμένες προς το επίπεδο βάσης κατά μία γωνία, τότε τα αποθέματα των πλευρικών όψεων είναι ίσα.
Ιδιότητες μιας κανονικής πυραμίδας
1. Η κορυφή της πυραμίδας έχει ίση απόσταση από όλες τις γωνίες της βάσης.
2. Όλες οι πλευρικές άκρες είναι ίσες.
3. Όλες οι πλευρικές νευρώσεις έχουν κλίση στις ίδιες γωνίες με τη βάση.
4. Τα αποθέματα όλων των πλευρικών όψεων είναι ίσα.
5. Τα εμβαδά όλων των πλευρικών όψεων είναι ίσα.
6. Όλες οι όψεις έχουν τις ίδιες δίεδρες (επίπεδες) γωνίες.
7. Μια σφαίρα μπορεί να περιγραφεί γύρω από την πυραμίδα. Το κέντρο της περιγραφόμενης σφαίρας θα είναι το σημείο τομής των κάθετων που διέρχονται από το μέσο των άκρων.
8. Μια σφαίρα μπορεί να εγγραφεί σε μια πυραμίδα. Το κέντρο της εγγεγραμμένης σφαίρας θα είναι το σημείο τομής των διχοτόμων που προέρχονται από τη γωνία μεταξύ της άκρης και της βάσης.
9. Εάν το κέντρο της εγγεγραμμένης σφαίρας συμπίπτει με το κέντρο της περιγεγραμμένης σφαίρας, τότε το άθροισμα των επίπεδων γωνιών στην κορυφή είναι ίσο με π ή αντίστροφα, μια γωνία είναι ίση με π / n, όπου n είναι ο αριθμός των γωνιών στη βάση της πυραμίδας.
Η σύνδεση της πυραμίδας με τη σφαίρα
Μια σφαίρα μπορεί να περιγραφεί γύρω από την πυραμίδα όταν στη βάση της πυραμίδας βρίσκεται ένα πολύεδρο γύρω από το οποίο μπορεί να περιγραφεί ένας κύκλος (απαραίτητη και επαρκής συνθήκη). Το κέντρο της σφαίρας θα είναι το σημείο τομής των επιπέδων που διέρχονται κάθετα από τα μέσα των πλευρικών άκρων της πυραμίδας.
Μια σφαίρα μπορεί πάντα να περιγραφεί γύρω από οποιαδήποτε τριγωνική ή κανονική πυραμίδα.
Μια σφαίρα μπορεί να εγγραφεί σε μια πυραμίδα εάν τα επίπεδα διχοτόμων των εσωτερικών διεδρικών γωνιών της πυραμίδας τέμνονται σε ένα σημείο (απαραίτητη και επαρκής συνθήκη). Αυτό το σημείο θα είναι το κέντρο της σφαίρας.
Η σύνδεση της πυραμίδας με τον κώνο
Ένας κώνος ονομάζεται εγγεγραμμένος σε μια πυραμίδα εάν οι κορυφές τους συμπίπτουν και η βάση του κώνου είναι εγγεγραμμένη στη βάση της πυραμίδας.
Ένας κώνος μπορεί να εγγραφεί σε μια πυραμίδα εάν τα αποθέματα της πυραμίδας είναι ίσα.
Ένας κώνος λέγεται ότι περιβάλλεται γύρω από μια πυραμίδα εάν οι κορυφές τους συμπίπτουν και η βάση του κώνου είναι περιγεγραμμένη γύρω από τη βάση της πυραμίδας.
Ένας κώνος μπορεί να περιγραφεί γύρω από μια πυραμίδα εάν όλες οι πλευρικές ακμές της πυραμίδας είναι ίσες μεταξύ τους.
Σύνδεση πυραμίδας με κύλινδρο
Μια πυραμίδα λέγεται ότι είναι εγγεγραμμένη σε έναν κύλινδρο εάν η κορυφή της πυραμίδας βρίσκεται σε μια βάση του κυλίνδρου και η βάση της πυραμίδας είναι εγγεγραμμένη σε μια άλλη βάση του κυλίνδρου.
Ένας κύλινδρος μπορεί να περιγραφεί γύρω από μια πυραμίδα εάν ένας κύκλος μπορεί να περιγραφεί γύρω από τη βάση της πυραμίδας.
Ένα τετράεδρο έχει τέσσερις όψεις και τέσσερις κορυφές και έξι ακμές, όπου οποιεσδήποτε δύο ακμές δεν έχουν κοινές κορυφές αλλά δεν ακουμπούν.
Κάθε κορυφή αποτελείται από τρεις όψεις και ακμές που σχηματίζονται τριεδρική γωνία.
Το τμήμα που συνδέει την κορυφή του τετραέδρου με το κέντρο της απέναντι όψης ονομάζεται διάμεσος του τετραέδρου(GM).
Διμέσοςονομάζεται τμήμα που συνδέει τα μέσα των απέναντι άκρων που δεν εφάπτονται (KL).
Όλα τα δίμεσα και οι διάμεσοι ενός τετραέδρου τέμνονται σε ένα σημείο (S). Σε αυτή την περίπτωση, τα δίμεσα χωρίζονται στο μισό και οι διάμεσοι σε αναλογία 3: 1 ξεκινώντας από την κορυφή.
Ορισμός. Οξεία γωνιακή πυραμίδαείναι μια πυραμίδα στην οποία το απόθεμα είναι περισσότερο από το μισό μήκος της πλευράς της βάσης.
Ορισμός. αμβλεία πυραμίδαείναι μια πυραμίδα στην οποία το απόθεμα είναι μικρότερο από το μισό μήκος της πλευράς της βάσης.
Ορισμός. κανονικό τετράεδροΈνα τετράεδρο του οποίου οι τέσσερις όψεις είναι ισόπλευρα τρίγωνα. Είναι ένα από τα πέντε κανονικά πολύγωνα. Σε ένα κανονικό τετράεδρο, όλες οι διεδρικές γωνίες (μεταξύ όψεων) και οι τριεδρικές γωνίες (σε μια κορυφή) είναι ίσες.
Ορισμός. Ορθογώνιο τετράεδροονομάζεται τετράεδρο που έχει ορθή γωνία μεταξύ τριών ακμών στην κορυφή (οι ακμές είναι κάθετες). Σχηματίζονται τρία πρόσωπα ορθογώνια τριεδρική γωνίακαι οι όψεις είναι ορθογώνια τρίγωνα, και η βάση είναι ένα αυθαίρετο τρίγωνο. Το απόθεμα οποιουδήποτε προσώπου ισούται με το ήμισυ της πλευράς της βάσης στην οποία πέφτει το απόθεμα.
Ορισμός. Ισοεδρικό τετράεδροΟνομάζεται τετράεδρο στο οποίο οι πλευρικές όψεις είναι ίσες μεταξύ τους και η βάση είναι ένα κανονικό τρίγωνο. Οι όψεις ενός τέτοιου τετραέδρου είναι ισοσκελές τρίγωνα.
Ορισμός. Ορθόκεντρο τετράεδρολέγεται τετράεδρο στο οποίο όλα τα ύψη (κάθετοι) που κατεβαίνουν από την κορυφή προς την απέναντι όψη τέμνονται σε ένα σημείο.
Ορισμός. πυραμίδα αστεριώνΈνα πολύεδρο του οποίου η βάση είναι ένα αστέρι ονομάζεται.
Σε μια κανονική τριγωνική πυραμίδα SABC R- μέση της πλευράς ΑΒ, μικρό- μπλουζα.
Είναι γνωστό ότι SR = 6, και η πλευρική επιφάνεια είναι 36
.
Βρείτε το μήκος του τμήματος προ ΧΡΙΣΤΟΥ.
Ας κάνουμε μια φάρσα. Σε μια κανονική πυραμίδα, οι πλευρικές όψεις είναι ισοσκελές τρίγωνα.
Ευθύγραμμο τμήμα SR- η μέση χαμηλώνει στη βάση, και ως εκ τούτου το ύψος της πλευρικής όψης.
Η πλευρική επιφάνεια μιας κανονικής τριγωνικής πυραμίδας είναι ίση με το άθροισμα των εμβαδών
τρεις ίσες πλευρές S πλευρά = 3 S ABS. Από εδώ S ABS = 36: 3 = 12- περιοχή προσώπου.
Το εμβαδόν ενός τριγώνου είναι το μισό γινόμενο της βάσης του επί το ύψος του.
S ABS = 0,5 AB SR. Γνωρίζοντας το εμβαδόν και το ύψος, βρίσκουμε την πλευρά της βάσης ΑΒ = Π.Χ.
12 = 0,5 AB 6
12 = 3 ΑΒ
ΑΒ = 4
Απάντηση: 4
Μπορείτε να προσεγγίσετε το πρόβλημα από την άλλη άκρη. Αφήστε την πλευρά της βάσης AB = BC = α.
Στη συνέχεια η περιοχή του προσώπου S ABS = 0,5 AB SR = 0,5 a 6 = 3a.
Το εμβαδόν καθενός από τα τρία πρόσωπα είναι 3α, το εμβαδόν των τριών όψεων είναι 9α.
Σύμφωνα με την κατάσταση του προβλήματος, το εμβαδόν της πλευρικής επιφάνειας της πυραμίδας είναι 36.
S πλευρά = 9a = 36.
Από εδώ α = 4.
- Σε επαφή με 0
- Google+ 0
- Εντάξει 0
- Facebook 0
