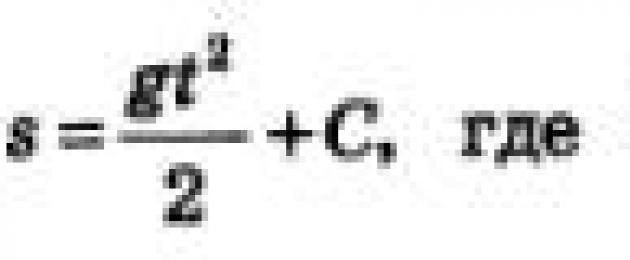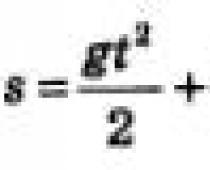Κανόνες εύρεσης αντιπαραγώγων. Αντιπαράγωγο. Μελετάμε την έννοια του "ολοκληρωτικού"

Στόχος:

1. Γνωρίστε τον ορισμό ενός αντιπαραγώγου, την κύρια ιδιότητα ενός αντιπαραγώγου, τους κανόνες για την εύρεση ενός αντιπαραγώγου.
2. Να είναι σε θέση να βρει τη γενική μορφή του αντιπαραγώγου.
3. Αναπτύξτε δεξιότητες αυτοελέγχου και ενδιαφέρον για το θέμα.
4. Καλλιεργήστε τη θέληση και την επιμονή για την επίτευξη τελικών αποτελεσμάτων κατά την ολοκλήρωση των εργασιών.

Κατά τη διάρκεια των μαθημάτων

Ι. Οργανωτική στιγμή.

II. Έλεγχος αφομοίωσης του μελετημένου υλικού.

1. Έρευνα με χρήση καρτών:

Α) Να διατυπώσετε τον ορισμό του αντιπαραγώγου;
Β) Να διατυπώσετε ένα σημάδι σταθερότητας συνάρτησης;
Ε) Να διατυπώσετε την κύρια ιδιότητα των αντιπαραγώγων;
Δ) Συνεχίστε τη φράση "Η διαφοροποίηση είναι ...."
Δ) Η ένταξη είναι…..
Ε) Οι γραφικές παραστάσεις οποιωνδήποτε δύο αντιπαραγώγων για τη συνάρτηση f λαμβάνονται μεταξύ τους…….
Ζ) Τι είναι αυτό;...

2. Βρείτε τη γενική μορφή των αντιπαραγώγων για τη συνάρτηση:

Α) f(x) = 1
Β) g(x) = x +1
Β) f (x) = cos (3x + 4)
Δ) g (x) = 2 cosx + 4
Δ) g (x) = sin x + cos x
Ε) F (x) = (x + 1)³

3. Από τις δεδομένες συναρτήσεις, επιλέξτε την αντιπαράγωγο για τις συναρτήσεις y = - 7x ³

III. Ομαδική δουλειά

1η ομάδα - παίζει πασιέντζα. Στα τραπέζια υπάρχουν κομμένες κάρτες. Φτιάξτε όλους τους τύπους που γνωρίζετε. Πόσες φορές στάθηκες τυχερός;

2η και 3η ομάδα - εργασία με λότο. Καταγράψτε τη λέξη-κλειδί που προκύπτει.

		f (x) = (x + 1)4	f(x) = 2x5- 3x2	f(x) = cos (3x +4)
f(x) = (7x – 2)8	f(x) = x4-x2+x-1			f(x) = 1 – cos3x

(λέξη κλειδί – αντιπαράγωγο)

4η ομάδα – δουλεύει με σταυρόλεξο.

Σταυρόλεξο.

Ερωτήσεις:

2. Ποια είναι η γραφική παράσταση της συνάρτησης y = ax + b.

4. Ποιο μάθημα γίνεται συνήθως πριν από το τεστ.

5. Συνώνυμο της λέξης δωδεκάδα.

6. Είναι σε κάθε λέξη, σε εξισώσεις και μπορεί να είναι σε εξισώσεις.

7. Τι μπορεί να υπολογιστεί χρησιμοποιώντας τον τύπο α β.

8. Μια από τις πιο σημαντικές έννοιες στα μαθηματικά.

9. Έντυπο του μαθήματος στο οποίο πραγματοποιείται το τεστ γνώσεων.

10. Γερμανός επιστήμονας που εισήγαγε τον ολοκληρωτικό λογισμό.

11. Το σύνολο των σημείων του επιπέδου με συντεταγμένες (x; y), όπου το x διατρέχει το πεδίο ορισμού της συνάρτησης f.

12. Οι αντιστοιχίες μεταξύ των συνόλων X και Y, στα οποία κάθε τιμή του συνόλου X συνδέεται με μία μόνο τιμή από το σύνολο Y, λέγονται...

Όταν λύνετε σωστά το σταυρόλεξο κάτω από τον αριθμό 1 κάθετα, διαβάστε τη λέξη-κλειδί.

IV. Ανάλυση εργασιών από την Ενιαία Κρατική Εξέταση σε αυτό το θέμα από προηγούμενα χρόνια.

Δείξτε την αντιπαράγωγο F της συνάρτησης f(x) = 3sin x αν είναι γνωστό ότι F(П) = 1.

V. Ανεξάρτητη εργασία.

Ομάδες 1 και 2 – εκτελέστε τη δοκιμή.

Μέρος Α

Α'1. Από αυτές τις συναρτήσεις, επιλέξτε αυτή της οποίας η παράγωγος είναι ίση με f(x) = 20x4.

1). F(x) = 4x5
2). F(x) =5x5
3).F(x) = x5
4). F(x) = 80x3

Α2. Να βρείτε τη γενική μορφή των αντιπαραγώγων για τη συνάρτηση f(x) = 4x3 – 6

1). F(x) = x4 -6x + 5
2).F(x) = x4 - 6x + C
3).F(x) = 12x2 + C
4). F(x) = 12x2 – 6

A3.Για τη συνάρτηση f(x) =8x – 3, να βρείτε την αντιπαράγωγο της οποίας η γραφική παράσταση διέρχεται από το σημείο M (1; 4).

1) F(x) = 4x2 – 3x
2) F(x) = 4x2 – 3x -51
3) F(x) = 4x2 – 3x + 4
4) F(x) = 4x2 - 3x +3

Α4. Να βρείτε τη γενική μορφή των αντιπαραγώγων για τη συνάρτηση f(x) = 2/x3

1) F(x) = 1/x +C
2) F(x) = - 2/x + C
3) F(x) = - 1/x2 + C
4) F(x) = 2/x2+ C

Α5. Η αντιπαράγωγος για τη συνάρτηση f(x) = sin x + 3x2 είναι η συνάρτηση

1) F(x) = sin x +x3 – 5
2) F(x) = -cos x – x2 -1
3) F(x) = -cos x + x3 -2
4) F(x) = -x3cos x -3

Α6. Η αντιπαράγωγος για τη συνάρτηση f(x) = 3sin x είναι η συνάρτηση

1) F(x) = - 3xcos 3x
2) F(x) = - cos 3x
3) F(x) = - 3cos 3x
4) F(x) = - 3cos x

Α7. Η αντιπαράγωγος για τη συνάρτηση f(x) = cos 2x είναι η συνάρτηση

1) F(x) = 0,5sin 2x
2) F(x) = 0,5sin x
3) F(x) = 2 αμαρτία 2x
4) F(x) = 2sin x

Α8. Αντιπαράγωγος για τη συνάρτηση f(x) = 2 sinx cosx για τη συνάρτηση

1) F(x) = 0,5 sin2x
2) F(x) = 0,5sinx
3) F(x) = 2 sin2x
4) F(x) = 2 sin x

Α9. Για τη συνάρτηση f(x) = 6/cos23x + 1, βρείτε μια αντιπαράγωγο της οποίας η γραφική παράσταση διέρχεται από το σημείο M (P/3, P/3).

1) F(x) = 2 tan 3x + x +P/3
2) F(x) = 2 tan 3x + x
3) F(x) = - 6tg 3x + x + P/3
4) F(x) = 6 tan 3x + x

Μέρος Β

ΣΕ 1. Η συνάρτηση F(x) είναι αντιπαράγωγος της συνάρτησης f(x) = x5 – 3x2 – 2. Βρείτε την F(1) αν F(- 1) = 0.

3η και 4η ομάδα - διορθώστε το λάθος.

α) F(x) = x5, a f(x) = 1/6x6
β) F(x) = 4x – x3, a f(x) = 1/6x6
γ) F(x) = sin x, a f(x) = - cos x
δ) F(x) = 15 cos x, a f(x) = - 15 cos x
ε) F(x) = x/3 + 6/x – 1, a f(x) = 1/3 – 6/x2 στο (0 ; +)
ζ) Για τη συνάρτηση f(x) = 10 sin 2x, βρείτε την αντιπαράγωγο της οποίας η γραφική παράσταση διέρχεται από το σημείο M (-3/2P; 0)

VI. Περίληψη μαθήματος.

Δ/Ζ Νο 348, ατομική εργασία: Να γίνει παρουσίαση του θέματος.

Αυτό το μάθημα είναι το πρώτο σε μια σειρά βίντεο για την ενσωμάτωση. Σε αυτό θα αναλύσουμε τι είναι ένα αντιπαράγωγο μιας συνάρτησης και επίσης θα μελετήσουμε τις στοιχειώδεις μεθόδους υπολογισμού αυτών των ίδιων των αντιπαραγώγων.

Στην πραγματικότητα, δεν υπάρχει τίποτα περίπλοκο εδώ: ουσιαστικά όλα καταλήγουν στην έννοια του παραγώγου, με την οποία θα πρέπει να είστε ήδη εξοικειωμένοι.

Θα σημειώσω αμέσως ότι επειδή αυτό είναι το πρώτο μάθημα στο νέο μας θέμα, σήμερα δεν θα υπάρχουν σύνθετοι υπολογισμοί και τύποι, αλλά αυτά που θα μάθουμε σήμερα θα αποτελέσουν τη βάση για πολύ πιο σύνθετους υπολογισμούς και κατασκευές κατά τον υπολογισμό σύνθετων ολοκληρωμάτων και περιοχών .

Επιπλέον, όταν ξεκινάμε να μελετάμε την ολοκλήρωση και τα ολοκληρώματα ειδικότερα, υποθέτουμε σιωπηρά ότι ο μαθητής είναι ήδη τουλάχιστον εξοικειωμένος με τις έννοιες των παραγώγων και έχει τουλάχιστον βασικές δεξιότητες στον υπολογισμό τους. Χωρίς σαφή κατανόηση αυτού, δεν υπάρχει απολύτως τίποτα να κάνουμε στην ενσωμάτωση.

Ωστόσο, εδώ βρίσκεται ένα από τα πιο κοινά και ύπουλα προβλήματα. Το γεγονός είναι ότι, όταν αρχίζουν να υπολογίζουν τα πρώτα τους αντιπαράγωγα, πολλοί μαθητές τα μπερδεύουν με τα παράγωγα. Ως αποτέλεσμα, γίνονται ανόητα και προσβλητικά λάθη κατά τη διάρκεια των εξετάσεων και της ανεξάρτητης εργασίας.

Επομένως, τώρα δεν θα δώσω έναν σαφή ορισμό του αντιπαραγώγου. Σε αντάλλαγμα, σας προτείνω να δείτε πώς υπολογίζεται χρησιμοποιώντας ένα απλό συγκεκριμένο παράδειγμα.

Τι είναι ένα αντιπαράγωγο και πώς υπολογίζεται;

Γνωρίζουμε αυτόν τον τύπο:

\[((\left(((x)^(n)) \right))^(\prime ))=n\cdot ((x)^(n-1))\]

Αυτή η παράγωγος υπολογίζεται απλά:

\[(f)"\left(x \right)=((\left(((x)^(3)) \right))^(\prime ))=3((x)^(2))\ ]

Ας δούμε προσεκτικά την έκφραση που προκύπτει και ας εκφράσουμε $((x)^(2))$:

\[((x)^(2))=\frac(((\αριστερά(((x)^(3)) \δεξιά))^(\prime )))(3)\]

Αλλά μπορούμε να το γράψουμε ως εξής, σύμφωνα με τον ορισμό μιας παραγώγου:

\[((x)^(2))=((\αριστερά(\frac(((x)^(3)))(3) \δεξιά))^(\prime ))\]

Και τώρα προσοχή: αυτό που μόλις σημειώσαμε είναι ο ορισμός του αντιπαραγώγου. Αλλά για να το γράψετε σωστά, πρέπει να γράψετε τα εξής:

Ας γράψουμε την παρακάτω έκφραση με τον ίδιο τρόπο:

Αν γενικεύσουμε αυτόν τον κανόνα, μπορούμε να εξαγάγουμε τον ακόλουθο τύπο:

\[((x)^(n))\to \frac(((x)^(n+1)))(n+1)\]

Τώρα μπορούμε να διατυπώσουμε έναν σαφή ορισμό.

Αντιπαράγωγο μιας συνάρτησης είναι μια συνάρτηση της οποίας η παράγωγος είναι ίση με την αρχική συνάρτηση.

Ερωτήσεις σχετικά με την αντιπαράγωγη συνάρτηση

Θα φαινόταν ένας αρκετά απλός και κατανοητός ορισμός. Ωστόσο, μόλις το ακούσει, ο προσεκτικός μαθητής θα έχει αμέσως πολλές ερωτήσεις:

1. Ας πούμε, εντάξει, αυτός ο τύπος είναι σωστός. Ωστόσο, σε αυτήν την περίπτωση, με $n=1$, έχουμε προβλήματα: το "μηδέν" εμφανίζεται στον παρονομαστή και δεν μπορούμε να διαιρέσουμε με το "μηδέν".
2. Ο τύπος περιορίζεται μόνο σε βαθμούς. Πώς να υπολογίσετε την αντιπαράγωγο, για παράδειγμα, του ημιτόνου, του συνημιτόνου και οποιασδήποτε άλλης τριγωνομετρίας, καθώς και των σταθερών.
3. Υπαρξιακό ερώτημα: είναι πάντα δυνατό να βρεθεί αντιπαράγωγο; Αν ναι, τότε τι γίνεται με το αντιπαράγωγο του αθροίσματος, της διαφοράς, του προϊόντος κ.λπ.;

Θα απαντήσω αμέσως στην τελευταία ερώτηση. Δυστυχώς, το αντιπαράγωγο, σε αντίθεση με το παράγωγο, δεν λαμβάνεται πάντα υπόψη. Δεν υπάρχει καθολικός τύπος με τον οποίο από οποιαδήποτε αρχική κατασκευή θα λάβουμε μια συνάρτηση που θα είναι ίση με αυτήν την παρόμοια κατασκευή. Όσο για τις δυνάμεις και τις σταθερές, θα μιλήσουμε για αυτό τώρα.

Επίλυση προβλημάτων με συναρτήσεις ισχύος

\[((x)^(-1))\to \frac(((x)^(-1+1)))(-1+1)=\frac(1)(0)\]

Όπως μπορείτε να δείτε, αυτός ο τύπος για $((x)^(-1))$ δεν λειτουργεί. Τίθεται το ερώτημα: τι λειτουργεί τότε; Δεν μπορούμε να μετρήσουμε $((x)^(-1))$; Φυσικά μπορούμε. Ας θυμηθούμε πρώτα αυτό:

\[((x)^(-1))=\frac(1)(x)\]

Τώρα ας σκεφτούμε: η παράγωγος της οποίας συνάρτηση είναι ίση με $\frac(1)(x)$. Προφανώς, κάθε μαθητής που έχει μελετήσει τουλάχιστον λίγο αυτό το θέμα θα θυμάται ότι αυτή η έκφραση είναι ίση με την παράγωγο του φυσικού λογάριθμου:

\[((\αριστερά(\ln x \δεξιά))^(\prime ))=\frac(1)(x)\]

Επομένως, μπορούμε να γράψουμε με σιγουριά τα εξής:

\[\frac(1)(x)=((x)^(-1))\to \ln x\]

Πρέπει να γνωρίζετε αυτόν τον τύπο, όπως ακριβώς και την παράγωγο μιας συνάρτησης ισχύος.

Λοιπόν τι γνωρίζουμε μέχρι τώρα:

• Για μια συνάρτηση ισχύος - $((x)^(n))\to \frac(((x)^(n+1)))(n+1)$
• Για μια σταθερά - $=const\to \cdot x$
• Μια ειδική περίπτωση μιας συνάρτησης ισχύος είναι $\frac(1)(x)\to \ln x$

Και αν αρχίσουμε να πολλαπλασιάζουμε και να διαιρούμε τις απλούστερες συναρτήσεις, πώς μπορούμε τότε να υπολογίσουμε την αντιπαράγωγο ενός γινομένου ή ενός πηλίκου. Δυστυχώς, οι αναλογίες με το παράγωγο ενός προϊόντος ή ενός πηλίκου δεν λειτουργούν εδώ. Δεν υπάρχει τυπική φόρμουλα. Για ορισμένες περιπτώσεις, υπάρχουν δύσκολες ειδικές φόρμουλες - θα τις γνωρίσουμε σε μελλοντικά μαθήματα βίντεο.

Ωστόσο, να θυμάστε: δεν υπάρχει γενικός τύπος παρόμοιος με τον τύπο για τον υπολογισμό της παραγώγου ενός πηλίκου και ενός προϊόντος.

Επίλυση πραγματικών προβλημάτων

Εργασία Νο. 1

Ας υπολογίσουμε κάθε μία από τις συναρτήσεις ισχύος ξεχωριστά:

\[((x)^(2))\to \frac(((x)^(3)))(3)\]

Επιστρέφοντας στην έκφρασή μας, γράφουμε τη γενική κατασκευή:

Πρόβλημα Νο 2

Όπως είπα ήδη, πρωτότυπα έργα και στοιχεία «to the point» δεν λαμβάνονται υπόψη. Ωστόσο, εδώ μπορείτε να κάνετε τα εξής:

Αναλύσαμε το κλάσμα στο άθροισμα δύο κλασμάτων.

Ας κάνουμε τα μαθηματικά:

Τα καλά νέα είναι ότι γνωρίζοντας τους τύπους για τον υπολογισμό των αντιπαραγώγων, μπορείτε ήδη να υπολογίσετε πιο πολύπλοκες δομές. Ωστόσο, ας πάμε παρακάτω και ας διευρύνουμε λίγο περισσότερο τις γνώσεις μας. Το γεγονός είναι ότι πολλές κατασκευές και εκφράσεις, οι οποίες, εκ πρώτης όψεως, δεν έχουν καμία σχέση με το $((x)^(n))$, μπορούν να αναπαρασταθούν ως δύναμη με λογικό εκθέτη, δηλαδή:

\[\sqrt(x)=((x)^(\frac(1)(2)))\]

\[\sqrt[n](x)=((x)^(\frac(1)(n)))\]

\[\frac(1)(((x)^(n)))=((x)^(-n))\]

Όλες αυτές οι τεχνικές μπορούν και πρέπει να συνδυαστούν. Οι εκφράσεις δύναμης μπορούν να είναι

• πολλαπλασιάζω (προσθήκη βαθμών).
• διαίρεση (αφαιρούνται οι μοίρες).
• πολλαπλασιάζω με μια σταθερά.
• και τα λοιπά.

Επίλυση εκφράσεων δύναμης με ορθολογικό εκθέτη

Παράδειγμα Νο. 1

Ας υπολογίσουμε κάθε ρίζα ξεχωριστά:

\[\sqrt(x)=((x)^(\frac(1)(2)))\to \frac(((x)^(\frac(1)(2)+1)))(\ frac(1)(2)+1)=\frac(((x)^(\frac(3)(2))))(\frac(3)(2))=\frac(2\cdot (( x)^(\frac(3)(2))))(3)\]

\[\sqrt(x)=((x)^(\frac(1)(4)))\to \frac(((x)^(\frac(1)(4)))(\frac( 1)(4)+1)=\frac(((x)^(\frac(5)(4))))(\frac(5)(4))=\frac(4\cdot ((x) ^(\frac(5)(4))))(5)\]

Συνολικά, ολόκληρη η κατασκευή μας μπορεί να γραφτεί ως εξής:

Παράδειγμα Νο. 2

\[\frac(1)(\sqrt(x))=((\left(\sqrt(x) \right))^(-1))=((\left(((x)^(\frac( 1)(2))) \δεξιά))^(-1))=((x)^(-\frac(1)(2)))\]

Επομένως παίρνουμε:

\[\frac(1)(((x)^(3)))=((x)^(-3))\to \frac(((x)^(-3+1)))(-3 +1)=\frac(((x)^(-2)))(-2)=-\frac(1)(2((x)^(2)))\]

Συνολικά, συλλέγοντας τα πάντα σε μια έκφραση, μπορούμε να γράψουμε:

Παράδειγμα Νο. 3

Αρχικά, σημειώνουμε ότι έχουμε ήδη υπολογίσει το $\sqrt(x)$:

\[\sqrt(x)\to \frac(4((x)^(\frac(5)(4))))(5)\]

\[((x)^(\frac(3)(2)))\to \frac(((x)^(\frac(3)(2)+1)))(\frac(3)(2 )+1)=\frac(2\cdot ((x)^(\frac(5)(2))))(5)\]

Ας ξαναγράψουμε:

Ελπίζω να μην εκπλήξω κανέναν αν πω ότι αυτό που μόλις μελετήσαμε είναι μόνο οι απλούστεροι υπολογισμοί των αντιπαραγώγων, οι πιο στοιχειώδεις κατασκευές. Ας δούμε τώρα ελαφρώς πιο περίπλοκα παραδείγματα, στα οποία, εκτός από τα αντιπαράγωγα του πίνακα, θα πρέπει επίσης να θυμάστε το σχολικό πρόγραμμα σπουδών, δηλαδή, συντομευμένους τύπους πολλαπλασιασμού.

Επίλυση πιο σύνθετων παραδειγμάτων

Εργασία Νο. 1

Ας θυμηθούμε τον τύπο για την τετραγωνική διαφορά:

\[((\αριστερά(a-b \δεξιά))^(2))=((a)^(2))-ab+((b)^(2))\]

Ας ξαναγράψουμε τη συνάρτησή μας:

Τώρα πρέπει να βρούμε το πρωτότυπο μιας τέτοιας συνάρτησης:

\[((x)^(\frac(2)(3)))\to \frac(3\cdot ((x)^(\frac(5)(3)))(5)\]

\[((x)^(\frac(1)(3)))\to \frac(3\cdot ((x)^(\frac(4)(3)))(4)\]

Ας τα βάλουμε όλα μαζί σε μια κοινή δομή:

Πρόβλημα Νο 2

Σε αυτήν την περίπτωση, πρέπει να επεκτείνουμε τον κύβο διαφοράς. Ας θυμηθούμε:

\[((\left(a-b \right))^(3))=((a)^(3))-3((a)^(2))\cdot b+3a\cdot ((b)^ (2))-((β)^(3))\]

Λαμβάνοντας υπόψη αυτό το γεγονός, μπορούμε να το γράψουμε ως εξής:

Ας μεταμορφώσουμε λίγο τη συνάρτησή μας:

Μετράμε όπως πάντα - για κάθε όρο ξεχωριστά:

\[((x)^(-3))\to \frac(((x)^(-2)))(-2)\]

\[((x)^(-2))\to \frac(((x)^(-1)))(-1)\]

\[((x)^(-1))\ έως \ln x\]

Ας γράψουμε την κατασκευή που προκύπτει:

Εργασία Νο. 3

Στην κορυφή έχουμε το τετράγωνο του αθροίσματος, ας το επεκτείνουμε:

\[\frac(((\left(x+\sqrt(x) \right))^(2)))(x)=\frac(((x)^(2))+2x\cdot \sqrt(x )+((\αριστερά(\sqrt(x) \δεξιά))^(2)))(x)=\]

\[=\frac(((x)^(2)))(x)+\frac(2x\sqrt(x))(x)+\frac(x)(x)=x+2((x) ^(\frac(1)(2)))+1\]

\[((x)^(\frac(1)(2)))\to \frac(2\cdot ((x)^(\frac(3)(2)))(3)\]

Ας γράψουμε την τελική λύση:

Τώρα προσοχή! Κάτι πολύ σημαντικό, που συνδέεται με τη μερίδα του λέοντος στα λάθη και τις παρεξηγήσεις. Γεγονός είναι ότι μέχρι τώρα, μετρώντας αντιπαράγωγα χρησιμοποιώντας παραγώγους και φέρνοντας μετασχηματισμούς, δεν σκεφτήκαμε με τι ισούται η παράγωγος μιας σταθεράς. Αλλά η παράγωγος μιας σταθεράς είναι ίση με «μηδέν». Αυτό σημαίνει ότι μπορείτε να γράψετε τις ακόλουθες επιλογές:

1. $((x)^(2))\to \frac(((x)^(3)))(3)$
2. $((x)^(2))\to \frac(((x)^(3)))(3)+1$
3. $((x)^(2))\to \frac(((x)^(3)))(3)+C$

Αυτό είναι πολύ σημαντικό να κατανοήσουμε: αν η παράγωγος μιας συνάρτησης είναι πάντα η ίδια, τότε η ίδια συνάρτηση έχει άπειρο αριθμό αντιπαραγώγων. Μπορούμε απλά να προσθέσουμε οποιουσδήποτε σταθερούς αριθμούς στα αντιπαράγωγά μας και να πάρουμε νέους.

Δεν είναι τυχαίο ότι στην εξήγηση των προβλημάτων που μόλις λύσαμε, γράφτηκε «Γράψε τη γενική μορφή των αντιπαραγώγων». Εκείνοι. Υποτίθεται ήδη εκ των προτέρων ότι δεν υπάρχει ένας από αυτούς, αλλά ένα ολόκληρο πλήθος. Αλλά, στην πραγματικότητα, διαφέρουν μόνο στη σταθερή $C$ στο τέλος. Επομένως, στα καθήκοντά μας θα διορθώσουμε αυτά που δεν ολοκληρώσαμε.

Για άλλη μια φορά ξαναγράφουμε τις κατασκευές μας:

Σε τέτοιες περιπτώσεις, θα πρέπει να προσθέσετε ότι το $C$ είναι μια σταθερά - $C=const$.

Στη δεύτερη συνάρτησή μας έχουμε την ακόλουθη κατασκευή:

Και το τελευταίο:

Και τώρα πήραμε πραγματικά αυτό που απαιτούνταν από εμάς στην αρχική κατάσταση του προβλήματος.

Επίλυση προβλημάτων εύρεσης αντιπαραγώγων με δεδομένο σημείο

Τώρα που γνωρίζουμε για τις σταθερές και τις ιδιαιτερότητες της γραφής αντιπαραγώγων, είναι πολύ λογικό να προκύπτει ο επόμενος τύπος προβλήματος όταν, από το σύνολο όλων των αντιπαραγώγων, απαιτείται να βρεθεί το ένα και μοναδικό που θα περνούσε από ένα δεδομένο σημείο . Τι είναι αυτό το καθήκον;

Το γεγονός είναι ότι όλα τα αντιπαράγωγα μιας δεδομένης συνάρτησης διαφέρουν μόνο στο ότι μετατοπίζονται κατακόρυφα κατά έναν ορισμένο αριθμό. Και αυτό σημαίνει ότι ανεξάρτητα από το σημείο στο επίπεδο συντεταγμένων που πάρουμε, σίγουρα θα περάσει ένα αντιπαράγωγο και, επιπλέον, μόνο ένα.

Έτσι, τα προβλήματα που θα λύσουμε τώρα διατυπώνονται ως εξής: όχι απλώς βρείτε την αντιπαράγωγο, γνωρίζοντας τον τύπο της αρχικής συνάρτησης, αλλά επιλέξτε ακριβώς αυτό που διέρχεται από το δεδομένο σημείο, οι συντεταγμένες του οποίου θα δοθούν στο πρόβλημα δήλωση.

Παράδειγμα Νο. 1

Αρχικά, ας μετρήσουμε απλώς κάθε όρο:

\[((x)^(4))\to \frac(((x)^(5)))(5)\]

\[((x)^(3))\to \frac(((x)^(4)))(4)\]

Τώρα αντικαθιστούμε αυτές τις εκφράσεις στην κατασκευή μας:

Αυτή η συνάρτηση πρέπει να περάσει από το σημείο $M\left(-1;4 \right)$. Τι σημαίνει ότι περνά από ένα σημείο; Αυτό σημαίνει ότι αν αντί για $x$ βάλουμε $-1$ παντού και αντί για $F\left(x \right)$ - $-4$, τότε θα πρέπει να έχουμε τη σωστή αριθμητική ισότητα. Ας το κάνουμε:

Βλέπουμε ότι έχουμε μια εξίσωση για $C$, οπότε ας προσπαθήσουμε να τη λύσουμε:

Ας γράψουμε τη λύση που αναζητούσαμε:

Παράδειγμα Νο. 2

Πρώτα απ 'όλα, είναι απαραίτητο να αποκαλύψουμε το τετράγωνο της διαφοράς χρησιμοποιώντας τον συντομευμένο τύπο πολλαπλασιασμού:

\[((x)^(2))\to \frac(((x)^(3)))(3)\]

Η αρχική κατασκευή θα γραφτεί ως εξής:

Τώρα ας βρούμε το $C$: αντικαταστήστε τις συντεταγμένες του σημείου $M$:

\[-1=\frac(8)(3)-12+18+C\]

Εκφράζουμε $C$:

Απομένει να εμφανιστεί η τελική έκφραση:

Επίλυση τριγωνομετρικών προβλημάτων

Ως τελευταία πινελιά σε αυτό που μόλις συζητήσαμε, προτείνω να εξετάσουμε δύο πιο σύνθετα προβλήματα που περιλαμβάνουν την τριγωνομετρία. Σε αυτές, με τον ίδιο τρόπο, θα χρειαστεί να βρείτε αντιπαράγωγα για όλες τις συναρτήσεις και, στη συνέχεια, να επιλέξετε από αυτό το σύνολο τη μοναδική που διέρχεται από το σημείο $M$ στο επίπεδο συντεταγμένων.

Κοιτάζοντας μπροστά, θα ήθελα να σημειώσω ότι η τεχνική που θα χρησιμοποιήσουμε τώρα για να βρούμε αντιπαράγωγα τριγωνομετρικών συναρτήσεων είναι, στην πραγματικότητα, μια καθολική τεχνική για αυτοέλεγχο.

Εργασία Νο. 1

Ας θυμηθούμε τον ακόλουθο τύπο:

\[((\αριστερά(\κείμενο(tg)x \δεξιά))^(\prime ))=\frac(1)(((\cos )^(2))x)\]

Με βάση αυτό, μπορούμε να γράψουμε:

Ας αντικαταστήσουμε τις συντεταγμένες του σημείου $M$ στην έκφρασή μας:

\[-1=\text(tg)\frac(\text( )\!\!\pi\!\!\text( ))(\text(4))+C\]

Ας ξαναγράψουμε την έκφραση λαμβάνοντας υπόψη αυτό το γεγονός:

Πρόβλημα Νο 2

Αυτό θα είναι λίγο πιο δύσκολο. Τώρα θα δείτε γιατί.

Ας θυμηθούμε αυτόν τον τύπο:

\[((\αριστερά(\κείμενο(ctg)x \δεξιά))^(\prime ))=-\frac(1)(((\sin )^(2))x)\]

Για να απαλλαγείτε από το "μείον", πρέπει να κάνετε τα εξής:

\[((\left(-\text(ctg)x \right))^(\prime ))=\frac(1)(((\sin )^(2))x)\]

Εδώ είναι το σχέδιό μας

Ας αντικαταστήσουμε τις συντεταγμένες του σημείου $M$:

Συνολικά, σημειώνουμε την τελική κατασκευή:

Μόνο αυτό ήθελα να σας πω σήμερα. Μελετήσαμε τον ίδιο τον όρο αντιπαράγωγα, πώς να τα υπολογίσουμε από στοιχειώδεις συναρτήσεις και επίσης πώς να βρούμε μια αντιπαράγωγο που διέρχεται από ένα συγκεκριμένο σημείο στο επίπεδο συντεταγμένων.

Ελπίζω ότι αυτό το μάθημα θα σας βοηθήσει να κατανοήσετε τουλάχιστον λίγο αυτό το περίπλοκο θέμα. Σε κάθε περίπτωση, πάνω στα αντιπαράγωγα κατασκευάζονται αόριστα και αόριστα ολοκληρώματα, επομένως είναι απολύτως απαραίτητος ο υπολογισμός τους. Αυτό είναι όλο για μένα. Τα λέμε!

Προηγουμένως, με δεδομένη μια δεδομένη συνάρτηση, καθοδηγούμενη από διάφορους τύπους και κανόνες, βρήκαμε την παράγωγό της. Το παράγωγο έχει πολλές χρήσεις: είναι η ταχύτητα κίνησης (ή, γενικότερα, η ταχύτητα οποιασδήποτε διαδικασίας). ο γωνιακός συντελεστής της εφαπτομένης στη γραφική παράσταση της συνάρτησης. χρησιμοποιώντας την παράγωγο, μπορείτε να εξετάσετε τη συνάρτηση για μονοτονία και ακρότατα. βοηθά στην επίλυση προβλημάτων βελτιστοποίησης.

Αλλά μαζί με το πρόβλημα της εύρεσης της ταχύτητας σύμφωνα με έναν γνωστό νόμο της κίνησης, υπάρχει επίσης ένα αντίστροφο πρόβλημα - το πρόβλημα της επαναφοράς του νόμου της κίνησης σύμφωνα με μια γνωστή ταχύτητα. Ας εξετάσουμε ένα από αυτά τα προβλήματα.

Παράδειγμα 1.Ένα υλικό σημείο κινείται σε ευθεία γραμμή, η ταχύτητά του τη χρονική στιγμή t δίνεται από τον τύπο v=gt. Βρείτε το νόμο της κίνησης.
Λύση. Έστω s = s(t) ο επιθυμητός νόμος της κίνησης. Είναι γνωστό ότι s"(t) = v(t). Αυτό σημαίνει ότι για να λύσετε το πρόβλημα πρέπει να επιλέξετε μια συνάρτηση s = s(t), η παράγωγος της οποίας είναι ίση με gt. Δεν είναι δύσκολο να μαντέψετε ότι \(s(t) = \frac(gt^ 2)(2)\).
\(s"(t) = \left(\frac(gt^2)(2) \right)" = \frac(g)(2)(t^2)" = \frac(g)(2) \ cdot 2t = gt\)
Απάντηση: \(s(t) = \frac(gt^2)(2) \)

Ας σημειώσουμε αμέσως ότι το παράδειγμα έχει λυθεί σωστά, αλλά ελλιπώς. Πήραμε \(s(t) = \frac(gt^2)(2) \). Στην πραγματικότητα, το πρόβλημα έχει άπειρες λύσεις: οποιαδήποτε συνάρτηση της μορφής \(s(t) = \frac(gt^2)(2) + C\), όπου το C είναι μια αυθαίρετη σταθερά, μπορεί να χρησιμεύσει ως νόμος του κίνηση, αφού \(\αριστερά (\frac(gt^2)(2) +C \δεξιά)" = gt \)

Για να κάνουμε το πρόβλημα πιο συγκεκριμένο, έπρεπε να διορθώσουμε την αρχική κατάσταση: να υποδείξουμε τη συντεταγμένη ενός κινούμενου σημείου σε κάποια χρονική στιγμή, για παράδειγμα στο t = 0. Αν, ας πούμε, s(0) = s 0, τότε από το ισότητα s(t) = (gt 2)/2 + C παίρνουμε: s(0) = 0 + C, δηλαδή C = s 0. Τώρα ο νόμος της κίνησης ορίζεται μοναδικά: s(t) = (gt 2)/2 + s 0.

Στα μαθηματικά, στις αμοιβαία αντίστροφες πράξεις δίνονται διαφορετικά ονόματα, επινοούνται ειδικοί συμβολισμοί, για παράδειγμα: τετραγωνισμός (x 2) και τετραγωνική ρίζα (\(\sqrt(x) \)), ημίτονο (sin x) και arcsine (arcsin x) και κλπ. Η διαδικασία εύρεσης της παραγώγου μιας δεδομένης συνάρτησης ονομάζεται ΔΙΑΦΟΡΕΤΙΚΟΤΗΤΑ-διάκριση, και η αντίστροφη πράξη, δηλαδή η διαδικασία εύρεσης μιας συνάρτησης από μια δεδομένη παράγωγο, είναι ενσωμάτωση.

Ο ίδιος ο όρος «παράγωγο» μπορεί να δικαιολογηθεί «με καθημερινούς όρους»: η συνάρτηση y = f(x) «γεννά» μια νέα συνάρτηση y" = f"(x). Η συνάρτηση y = f(x) λειτουργεί ως «γονέας», αλλά οι μαθηματικοί, φυσικά, δεν την αποκαλούν «γονέα» ή «παραγωγό» λένε ότι είναι, σε σχέση με τη συνάρτηση y" = f"( x) , κύρια εικόνα ή πρωτόγονη.

Ορισμός.Η συνάρτηση y = F(x) ονομάζεται αντιπαράγωγος για τη συνάρτηση y = f(x) στο διάστημα X αν η ισότητα F"(x) = f(x) ισχύει για \(x \σε X\)

Στην πράξη, το διάστημα X συνήθως δεν προσδιορίζεται, αλλά υπονοείται (ως το φυσικό πεδίο ορισμού της συνάρτησης).

Ας δώσουμε παραδείγματα.
1) Η συνάρτηση y = x 2 είναι αντιπαράγωγος για τη συνάρτηση y = 2x, αφού για κάθε x η ισότητα (x 2)" = 2x είναι αληθής
2) Η συνάρτηση y = x 3 είναι αντιπαράγωγος για τη συνάρτηση y = 3x 2, αφού για κάθε x η ισότητα (x 3)" = 3x 2 είναι αληθής
3) Η συνάρτηση y = sin(x) είναι αντιπαράγωγος για τη συνάρτηση y = cos(x), αφού για κάθε x η ισότητα (sin(x))" = cos(x) είναι αληθής

Κατά την εύρεση αντιπαραγώγων, καθώς και παραγώγων, δεν χρησιμοποιούνται μόνο τύποι, αλλά και ορισμένοι κανόνες. Σχετίζονται άμεσα με τους αντίστοιχους κανόνες για τον υπολογισμό των παραγώγων.

Γνωρίζουμε ότι η παράγωγος ενός αθροίσματος είναι ίση με το άθροισμα των παραγώγων του. Αυτός ο κανόνας δημιουργεί τον αντίστοιχο κανόνα για την εύρεση αντιπαραγώγων.

Κανόνας 1.Το αντιπαράγωγο ενός αθροίσματος είναι ίσο με το άθροισμα των αντιπαραγώγων.

Γνωρίζουμε ότι ο σταθερός παράγοντας μπορεί να αφαιρεθεί από το πρόσημο της παραγώγου. Αυτός ο κανόνας δημιουργεί τον αντίστοιχο κανόνα για την εύρεση αντιπαραγώγων.

Κανόνας 2.Εάν το F(x) είναι ένα αντιπαράγωγο για το f(x), τότε το kF(x) είναι ένα αντιπαράγωγο για το kf(x).

Θεώρημα 1.Αν το y = F(x) είναι αντιπαράγωγος για τη συνάρτηση y = f(x), τότε το αντιπαράγωγο για τη συνάρτηση y = f(kx + m) είναι η συνάρτηση \(y=\frac(1)(k)F (kx+m) \)

Θεώρημα 2.Αν το y = F(x) είναι αντιπαράγωγο για τη συνάρτηση y = f(x) στο διάστημα X, τότε η συνάρτηση y = f(x) έχει άπειρα πολλά αντιπαράγωγα και όλα έχουν τη μορφή y = F(x) + Γ.

Μέθοδοι ολοκλήρωσης

Μέθοδος αντικατάστασης μεταβλητής (μέθοδος αντικατάστασης)

Η μέθοδος ολοκλήρωσης με υποκατάσταση περιλαμβάνει την εισαγωγή μιας νέας μεταβλητής ολοκλήρωσης (δηλαδή υποκατάστασης). Σε αυτήν την περίπτωση, το δεδομένο ολοκλήρωμα ανάγεται σε ένα νέο ολοκλήρωμα, το οποίο είναι πίνακας ή αναγώγιμο σε αυτό. Δεν υπάρχουν γενικές μέθοδοι για την επιλογή αντικαταστάσεων. Η ικανότητα ορθού προσδιορισμού της υποκατάστασης αποκτάται μέσω της εξάσκησης.
Ας είναι απαραίτητο να υπολογιστεί το ολοκλήρωμα \(\textstyle \int F(x)dx \). Ας κάνουμε την αντικατάσταση \(x= \varphi(t) \) όπου \(\varphi(t) \) είναι μια συνάρτηση που έχει συνεχή παράγωγο.
Στη συνέχεια, \(dx = \varphi " (t) \cdot dt \) και με βάση την ιδιότητα αμετάβλητης του τύπου ολοκλήρωσης για το αόριστο ολοκλήρωμα, λαμβάνουμε τον τύπο ολοκλήρωσης με αντικατάσταση:
\(\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt \)

Ενσωμάτωση εκφράσεων της μορφής \(\textstyle \int \sin^n x \cos^m x dx \)

Αν το m είναι περιττό, m > 0, τότε είναι πιο βολικό να γίνει η αντικατάσταση sin x = t.
Αν το n είναι περιττό, n > 0, τότε είναι πιο βολικό να γίνει η αντικατάσταση cos x = t.
Αν τα n και m είναι άρτια, τότε είναι πιο βολικό να γίνει η αντικατάσταση tg x = t.

Ενσωμάτωση κατά εξαρτήματα

Ενσωμάτωση ανά εξαρτήματα - εφαρμόζοντας τον ακόλουθο τύπο για ενσωμάτωση:
\(\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du \)
ή:
\(\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx \)

Πίνακας αόριστων ολοκληρωμάτων (αντιπαράγωγα) ορισμένων συναρτήσεων

$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) +C \;\; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(arcsin) x +C $$ $$ \int \frac(dx)(1+x^2 ) = \text(arctg) x +C $$ $$ \int \text(ch) x dx = \text(sh) x +C $$ $$ \int \text(sh) x dx = \text(ch ) x +C $$

Είδαμε ότι η παράγωγος έχει πολλές χρήσεις: η παράγωγος είναι η ταχύτητα κίνησης (ή, γενικότερα, η ταχύτητα οποιασδήποτε διαδικασίας). παράγωγος είναι η κλίση της εφαπτομένης στη γραφική παράσταση της συνάρτησης. χρησιμοποιώντας την παράγωγο, μπορείτε να εξετάσετε τη συνάρτηση για μονοτονία και ακρότατα. η παράγωγος βοηθά στην επίλυση προβλημάτων βελτιστοποίησης.

Αλλά στην πραγματική ζωή πρέπει επίσης να λύσουμε αντίστροφα προβλήματα: για παράδειγμα, μαζί με το πρόβλημα εύρεσης της ταχύτητας σύμφωνα με έναν γνωστό νόμο κίνησης, αντιμετωπίζουμε επίσης το πρόβλημα της επαναφοράς του νόμου της κίνησης σύμφωνα με μια γνωστή ταχύτητα. Ας εξετάσουμε ένα από αυτά τα προβλήματα.

Παράδειγμα 1.Ένα υλικό σημείο κινείται σε ευθεία γραμμή, η ταχύτητά του τη χρονική στιγμή t δίνεται από τον τύπο u = tg. Βρείτε το νόμο της κίνησης.

Λύση.Έστω s = s(t) ο επιθυμητός νόμος της κίνησης. Είναι γνωστό ότι s"(t) = u"(t). Αυτό σημαίνει ότι για να λύσετε το πρόβλημα πρέπει να επιλέξετε λειτουργία s = s(t), του οποίου η παράγωγος είναι ίση με tg. Δεν είναι δύσκολο να το μαντέψει κανείς αυτό

Ας σημειώσουμε αμέσως ότι το παράδειγμα έχει λυθεί σωστά, αλλά ελλιπώς. Βρήκαμε ότι, στην πραγματικότητα, το πρόβλημα έχει άπειρες λύσεις: οποιαδήποτε συνάρτηση της μορφής μια αυθαίρετη σταθερά μπορεί να χρησιμεύσει ως νόμος κίνησης, αφού

Για να κάνουμε την εργασία πιο συγκεκριμένη, χρειαζόταν να διορθώσουμε την αρχική κατάσταση: να υποδείξουμε τη συντεταγμένη ενός κινούμενου σημείου σε κάποια χρονική στιγμή, για παράδειγμα, στο t=0. Αν, ας πούμε, s(0) = s 0, τότε από την ισότητα παίρνουμε s(0) = 0 + C, δηλ. S 0 = C. Τώρα ο νόμος της κίνησης ορίζεται μοναδικά:
Στα μαθηματικά, στις αμοιβαία αντίστροφες πράξεις δίνονται διαφορετικά ονόματα και επινοούνται ειδικοί συμβολισμοί: για παράδειγμα, τετραγωνισμός (x 2) και λήψη της τετραγωνικής ρίζας του ημιτόνου (sinх) και τόξο(arcsin x) κ.λπ. Η διαδικασία εύρεσης της παραγώγου μιας δεδομένης συνάρτησης ονομάζεται διαφοροποίηση και η αντίστροφη πράξη, δηλ. η διαδικασία εύρεσης συνάρτησης από μια δεδομένη παράγωγο - ολοκλήρωση.
Ο ίδιος ο όρος «παράγωγος» μπορεί να δικαιολογηθεί «στην καθημερινή ζωή»: η συνάρτηση y - f(x) «γεννά» μια νέα συνάρτηση y"= f"(x). ένας «γονέας» , αλλά οι μαθηματικοί, φυσικά, δεν το αποκαλούν «γονέα» ή «παραγωγό» λένε ότι αυτή, σε σχέση με τη συνάρτηση y"=f"(x), είναι η κύρια εικόνα, ή, μέσα σύντομη, το αντιπαράγωγο.

Ορισμός 1.Η συνάρτηση y = F(x) ονομάζεται αντιπαράγωγος για τη συνάρτηση y = f(x) σε ένα δεδομένο διάστημα X αν για όλα τα x από το X ισχύει η ισότητα F"(x)=f(x).

Στην πράξη, το διάστημα X συνήθως δεν προσδιορίζεται, αλλά υπονοείται (ως το φυσικό πεδίο ορισμού της συνάρτησης).

Να μερικά παραδείγματα:

1) Η συνάρτηση y = x 2 είναι αντιπαράγωγος για τη συνάρτηση y = 2x, αφού για όλα τα x η ισότητα (x 2)" = 2x είναι αληθής.
2) η συνάρτηση y - x 3 είναι αντιπαράγωγος για τη συνάρτηση y-3x 2, αφού για όλα τα x ισχύει η ισότητα (x 3)" = 3x 2.
3) Η συνάρτηση y-sinх είναι αντιπαράγωγος για τη συνάρτηση y = cosx, αφού για όλα τα x ισχύει η ισότητα (sinx)" = cosx.
4) Η συνάρτηση είναι αντιπαράγωγος για μια συνάρτηση στο διάστημα αφού για όλα τα x > 0 η ισότητα είναι αληθής
Γενικά, γνωρίζοντας τους τύπους για την εύρεση παραγώγων, δεν είναι δύσκολο να συντάξουμε έναν πίνακα τύπων για την εύρεση αντιπαραγώγων.

Ελπίζουμε να καταλαβαίνετε πώς συντάσσεται αυτός ο πίνακας: η παράγωγος της συνάρτησης, που είναι γραμμένη στη δεύτερη στήλη, είναι ίση με τη συνάρτηση που είναι γραμμένη στην αντίστοιχη σειρά της πρώτης στήλης (ελέγξτε το, μην είστε τεμπέλης, είναι πολύ χρήσιμο). Για παράδειγμα, για τη συνάρτηση y = x 5 η αντιπαράγωγος, όπως θα καθορίσετε, είναι η συνάρτηση (δείτε την τέταρτη σειρά του πίνακα).

Σημειώσεις: 1. Παρακάτω θα αποδείξουμε το θεώρημα ότι αν y = F(x) είναι αντιπαράγωγος για τη συνάρτηση y = f(x), τότε η συνάρτηση y = f(x) έχει άπειρα πολλά αντιπαράγωγα και όλα έχουν τη μορφή y = F(x ) + C. Επομένως, θα ήταν πιο σωστό να προσθέσουμε τον όρο C παντού στη δεύτερη στήλη του πίνακα, όπου το C είναι ένας αυθαίρετος πραγματικός αριθμός.
2. Για λόγους συντομίας, μερικές φορές αντί για τη φράση «η συνάρτηση y = F(x) είναι αντιπαράγωγο της συνάρτησης y = f(x),» λένε ότι η F(x) είναι αντιπαράγωγος της f(x) .»

2. Κανόνες εύρεσης αντιπαραγώγων

Κατά την εύρεση αντιπαραγώγων, καθώς και κατά την εύρεση παραγώγων, δεν χρησιμοποιούνται μόνο τύποι (παρατίθενται στον πίνακα στη σελ. 196), αλλά και ορισμένοι κανόνες. Σχετίζονται άμεσα με τους αντίστοιχους κανόνες για τον υπολογισμό των παραγώγων.

Γνωρίζουμε ότι η παράγωγος ενός αθροίσματος είναι ίση με το άθροισμα των παραγώγων του. Αυτός ο κανόνας δημιουργεί τον αντίστοιχο κανόνα για την εύρεση αντιπαραγώγων.

Κανόνας 1.Το αντιπαράγωγο ενός αθροίσματος είναι ίσο με το άθροισμα των αντιπαραγώγων.

Εφιστούμε την προσοχή σας στην κάπως «ελαφρότητα» αυτής της διατύπωσης. Στην πραγματικότητα, θα πρέπει να διατυπωθεί το θεώρημα: εάν οι συναρτήσεις y = f(x) και y = g(x) έχουν αντιπαράγωγα στο διάστημα X, αντίστοιχα y-F(x) και y-G(x), τότε το άθροισμα των συναρτήσεων y = η f(x)+g(x) έχει μια αντιπαράγωγο στο διάστημα X, και αυτή η αντιπαράγωγος είναι η συνάρτηση y = F(x)+G(x). Αλλά συνήθως, κατά τη διατύπωση κανόνων (όχι θεωρημάτων), απομένουν μόνο λέξεις-κλειδιά - αυτό είναι πιο βολικό για την εφαρμογή των κανόνων στην πράξη

Παράδειγμα 2.Να βρείτε την αντιπαράγωγο για τη συνάρτηση y = 2x + cos x.

Λύση.Το αντιπαράγωγο για το 2x είναι x"· το αντιπαράγωγο για το cox είναι το sin x. Αυτό σημαίνει ότι το αντιπαράγωγο για τη συνάρτηση y = 2x + cos x θα είναι η συνάρτηση y = x 2 + sin x (και γενικά οποιαδήποτε συνάρτηση της μορφής Υ = x 1 + sinx + C) .
Γνωρίζουμε ότι ο σταθερός παράγοντας μπορεί να αφαιρεθεί από το πρόσημο της παραγώγου. Αυτός ο κανόνας δημιουργεί τον αντίστοιχο κανόνα για την εύρεση αντιπαραγώγων.

Κανόνας 2.Ο σταθερός παράγοντας μπορεί να αφαιρεθεί από το πρόσημο του αντιπαραγώγου.

Παράδειγμα 3.

Λύση.α) Το αντιπαράγωγο για το sin x είναι -soz x; Αυτό σημαίνει ότι για τη συνάρτηση y = 5 sin x η αντιπαράγωγη συνάρτηση θα είναι η συνάρτηση y = -5 cos x.

β) Το αντιπαράγωγο για το cos x είναι το sin x. Αυτό σημαίνει ότι το αντιπαράγωγο μιας συνάρτησης είναι η συνάρτηση
γ) Το αντιπαράγωγο για το x 3 είναι το αντιπαράγωγο για το x είναι το αντιπαράγωγο για τη συνάρτηση y = 1 είναι η συνάρτηση y = x. Χρησιμοποιώντας τον πρώτο και τον δεύτερο κανόνα για την εύρεση αντιπαραγώγων, βρίσκουμε ότι η αντιπαράγωγος για τη συνάρτηση y = 12x 3 + 8x-1 είναι η συνάρτηση
Σχόλιο.Όπως είναι γνωστό, το παράγωγο ενός προϊόντος δεν είναι ίσο με το γινόμενο των παραγώγων (ο κανόνας για τη διαφοροποίηση ενός προϊόντος είναι πιο σύνθετος) και το παράγωγο ενός πηλίκου δεν είναι ίσο με το πηλίκο των παραγώγων. Επομένως, δεν υπάρχουν κανόνες για την εύρεση του αντιπαραγώγου του προϊόντος ή του αντιπαραγώγου του πηλίκου δύο συναρτήσεων. Πρόσεχε!
Ας αποκτήσουμε έναν άλλο κανόνα για την εύρεση αντιπαραγώγων. Γνωρίζουμε ότι η παράγωγος της συνάρτησης y = f(kx+m) υπολογίζεται από τον τύπο

Αυτός ο κανόνας δημιουργεί τον αντίστοιχο κανόνα για την εύρεση αντιπαραγώγων.
Κανόνας 3.Αν το y = F(x) είναι αντιπαράγωγος για τη συνάρτηση y = f(x), τότε το αντιπαράγωγο για τη συνάρτηση y=f(kx+m) είναι η συνάρτηση

Πράγματι,

Αυτό σημαίνει ότι είναι αντιπαράγωγος για τη συνάρτηση y = f(kx+m).
Η έννοια του τρίτου κανόνα είναι η εξής. Εάν γνωρίζετε ότι η αντιπαράγωγος της συνάρτησης y = f(x) είναι η συνάρτηση y = F(x), και πρέπει να βρείτε την αντιπαράγωγο της συνάρτησης y = f(kx+m), τότε προχωρήστε ως εξής: πάρτε την ίδια συνάρτηση F, αλλά αντί για το όρισμα x, αντικαταστήστε την έκφραση kx+m. Επιπλέον, μην ξεχάσετε να γράψετε "συντελεστής διόρθωσης" πριν από το σύμβολο συνάρτησης
Παράδειγμα 4.Βρείτε αντιπαράγωγα για δεδομένες συναρτήσεις:

Λύση, α) Το αντιπαράγωγο για το sin x είναι -soz x; Αυτό σημαίνει ότι για τη συνάρτηση y = sin2x η αντιπαράγωγος θα είναι η συνάρτηση
β) Το αντιπαράγωγο για το cos x είναι το sin x. Αυτό σημαίνει ότι το αντιπαράγωγο μιας συνάρτησης είναι η συνάρτηση

γ) Η αντιπαράγωγος για το x 7 σημαίνει ότι για τη συνάρτηση y = (4-5x) 7 η αντιπαράγωγος θα είναι η συνάρτηση

3. Αόριστο ολοκλήρωμα

Έχουμε ήδη σημειώσει παραπάνω ότι το πρόβλημα της εύρεσης αντιπαραγώγου για μια δεδομένη συνάρτηση y = f(x) έχει περισσότερες από μία λύσεις. Ας συζητήσουμε αυτό το θέμα με περισσότερες λεπτομέρειες.

Απόδειξη. 1. Έστω y = F(x) η αντιπαράγωγος για τη συνάρτηση y = f(x) στο διάστημα X. Αυτό σημαίνει ότι για όλα τα x από το X ισχύει η ισότητα x"(x) = f(x). Ας βρείτε την παράγωγο οποιασδήποτε συνάρτησης της μορφής y = F(x)+C:
(F(x) +C) = F"(x) +C = f(x) +0 = f(x).

Άρα, (F(x)+C) = f(x). Αυτό σημαίνει ότι το y = F(x) + C είναι αντιπαράγωγο για τη συνάρτηση y = f(x).
Έτσι, αποδείξαμε ότι αν η συνάρτηση y = f(x) έχει αντιπαράγωγο y=F(x), τότε η συνάρτηση (f = f(x) έχει άπειρα πολλά αντιπαράγωγα, για παράδειγμα, οποιαδήποτε συνάρτηση της μορφής y = Το F(x) +C είναι ένα αντιπαράγωγο.
2. Ας αποδείξουμε τώρα ότι ο υποδεικνυόμενος τύπος συναρτήσεων εξαντλεί ολόκληρο το σύνολο των αντιπαραγώγων.

Έστω y=F 1 (x) και y=F(x) δύο αντιπαράγωγα για τη συνάρτηση Y = f(x) στο διάστημα X. Αυτό σημαίνει ότι για όλα τα x από το διάστημα X ισχύουν οι ακόλουθες σχέσεις: F^ ( x) = f (X); F"(x) = f(x).

Ας θεωρήσουμε τη συνάρτηση y = F 1 (x) -.F(x) και ας βρούμε την παράγωγό της: (F, (x) -F(x))" = F[(x)-F(x) = f(x ) - f(x) = 0.
Είναι γνωστό ότι αν η παράγωγος μιας συνάρτησης σε ένα διάστημα Χ είναι ταυτόσημη με μηδέν, τότε η συνάρτηση είναι σταθερή στο διάστημα Χ (βλ. Θεώρημα 3 από § 35). Αυτό σημαίνει ότι F 1 (x) - F (x) = C, δηλ. Fx) = F(x)+C.

Το θεώρημα είναι αποδεδειγμένο.

Παράδειγμα 5.Δίνεται ο νόμος της μεταβολής της ταχύτητας με το χρόνο: v = -5sin2t. Να βρείτε τον νόμο της κίνησης s = s(t), αν είναι γνωστό ότι τη χρονική στιγμή t=0 η συντεταγμένη του σημείου ήταν ίση με τον αριθμό 1,5 (δηλαδή s(t) = 1,5).

Λύση.Εφόσον η ταχύτητα είναι παράγωγος της συντεταγμένης σε συνάρτηση με το χρόνο, πρέπει πρώτα να βρούμε την αντιπαράγωγο της ταχύτητας, δηλ. αντιπαράγωγο για τη συνάρτηση v = -5sin2t. Ένα από αυτά τα αντιπαράγωγα είναι η συνάρτηση και το σύνολο όλων των αντιπαραγώγων έχει τη μορφή:

Για να βρούμε τη συγκεκριμένη τιμή της σταθεράς C, χρησιμοποιούμε τις αρχικές συνθήκες, σύμφωνα με τις οποίες s(0) = 1,5. Αντικαθιστώντας τις τιμές t=0, S = 1,5 στον τύπο (1), παίρνουμε:

Αντικαθιστώντας την ευρεθείσα τιμή του C στον τύπο (1), παίρνουμε τον νόμο της κίνησης που μας ενδιαφέρει:

Ορισμός 2.Αν μια συνάρτηση y = f(x) έχει αντιπαράγωγο y = F(x) σε ένα διάστημα Χ, τότε το σύνολο όλων των αντιπαραγώγων, δηλ. το σύνολο των συναρτήσεων της μορφής y = F(x) + C ονομάζεται αόριστο ολοκλήρωμα της συνάρτησης y = f(x) και συμβολίζεται με:

(διαβάστε: «αόριστο ολοκλήρωμα εφ από x de x»).
Στην επόμενη παράγραφο θα μάθουμε ποιο είναι το κρυφό νόημα αυτού του χαρακτηρισμού.
Με βάση τον πίνακα των αντιπαραγώγων που διατίθενται σε αυτήν την ενότητα, θα συντάξουμε έναν πίνακα με τα κύρια αόριστα ολοκληρώματα:

Με βάση τους παραπάνω τρεις κανόνες για την εύρεση αντιπαραγώγων, μπορούμε να διατυπώσουμε τους αντίστοιχους κανόνες ολοκλήρωσης.

Κανόνας 1.Το ολοκλήρωμα του αθροίσματος των συναρτήσεων είναι ίσο με το άθροισμα των ολοκληρωμάτων αυτών των συναρτήσεων:

Κανόνας 2.Ο σταθερός παράγοντας μπορεί να αφαιρεθεί από το ολοκλήρωμα:

Κανόνας 3.Αν

Παράδειγμα 6.Βρείτε αόριστα ολοκληρώματα:

Λύση, α) Χρησιμοποιώντας τον πρώτο και τον δεύτερο κανόνα ολοκλήρωσης, λαμβάνουμε:

Τώρα ας χρησιμοποιήσουμε τους τύπους 3ης και 4ης ολοκλήρωσης:

Ως αποτέλεσμα παίρνουμε:

β) Χρησιμοποιώντας τον τρίτο κανόνα ολοκλήρωσης και τον τύπο 8, λαμβάνουμε:

γ) Για να βρούμε άμεσα ένα ολοκλήρωμα, δεν έχουμε ούτε τον αντίστοιχο τύπο ούτε τον αντίστοιχο κανόνα. Σε τέτοιες περιπτώσεις, μερικές φορές βοηθούν οι προηγούμενοι πανομοιότυποι μετασχηματισμοί της έκφρασης που περιέχονται κάτω από το ολοκλήρωμα.

Ας χρησιμοποιήσουμε τον τριγωνομετρικό τύπο για τη μείωση του βαθμού:

Στη συνέχεια βρίσκουμε διαδοχικά:

Ο Α.Γ. Mordkovich Algebra 10η τάξη

Ημερολογιακός-θεματικός προγραμματισμός στα μαθηματικά, βίντεοστα μαθηματικά online, τα μαθηματικά στο σχολείο

Υπάρχουν τρεις βασικοί κανόνες για την εύρεση αντιπαραγώγων συναρτήσεων. Μοιάζουν πολύ με τους αντίστοιχους κανόνες διαφοροποίησης.

Κανόνας 1

Αν το F είναι αντιπαράγωγο για κάποια συνάρτηση f και το G είναι αντιπαράγωγο για κάποια συνάρτηση g, τότε το F + G θα είναι αντιπαράγωγο για τη f + g.

Εξ ορισμού αντιπαράγωγου, F’ = f. Ζ' = ζ. Και εφόσον πληρούνται αυτές οι προϋποθέσεις, τότε σύμφωνα με τον κανόνα για τον υπολογισμό της παραγώγου για το άθροισμα των συναρτήσεων θα έχουμε:

(F + G)’ = F’ + G’ = f + g.

Κανόνας 2

Αν το F είναι αντιπαράγωγο για κάποια συνάρτηση f, και το k είναι κάποια σταθερά. Τότε το k*F είναι αντιπαράγωγο για τη συνάρτηση k*f. Αυτός ο κανόνας προκύπτει από τον κανόνα για τον υπολογισμό της παραγώγου μιας μιγαδικής συνάρτησης.

Έχουμε: (k*F)’ = k*F’ = k*f.

Κανόνας 3

Αν η F(x) είναι κάποια αντιπαράγωγος για τη συνάρτηση f(x), και τα k και b είναι μερικές σταθερές, και το k δεν είναι ίσο με μηδέν, τότε το (1/k)*F*(k*x+b) θα είναι αντιπαράγωγο για τη συνάρτηση f (k*x+b).

Αυτός ο κανόνας προκύπτει από τον κανόνα για τον υπολογισμό της παραγώγου μιας μιγαδικής συνάρτησης:

((1/k)*F*(k*x+b))’ = (1/k)*F’(k*x+b)*k = f(k*x+b).

Ας δούμε μερικά παραδείγματα για το πώς εφαρμόζονται αυτοί οι κανόνες:

Παράδειγμα 1. Να βρείτε τη γενική μορφή των αντιπαραγώγων για τη συνάρτηση f(x) = x^3 +1/x^2. Για τη συνάρτηση x^3 ένα από τα αντιπαράγωγα θα είναι η συνάρτηση (x^4)/4 και για τη συνάρτηση 1/x^2 ένα από τα αντιπαράγωγα θα είναι η συνάρτηση -1/x. Χρησιμοποιώντας τον πρώτο κανόνα, έχουμε:

F(x) = x^4/4 - 1/x +C.

Παράδειγμα 2. Ας βρούμε τη γενική μορφή των αντιπαραγώγων για τη συνάρτηση f(x) = 5*cos(x). Για τη συνάρτηση cos(x), ένα από τα αντιπαράγωγα θα είναι η συνάρτηση sin(x). Εάν χρησιμοποιήσουμε τώρα τον δεύτερο κανόνα, θα έχουμε:

F(x) = 5*sin(x).

Παράδειγμα 3.Βρείτε ένα από τα αντιπαράγωγα για τη συνάρτηση y = sin(3*x-2). Για τη συνάρτηση sin(x) ένα από τα αντιπαράγωγα θα είναι η συνάρτηση -cos(x). Εάν χρησιμοποιήσουμε τώρα τον τρίτο κανόνα, λαμβάνουμε μια έκφραση για το αντιπαράγωγο:

F(x) = (-1/3)*cos(3*x-2)

Παράδειγμα 4. Βρείτε την αντιπαράγωγο για τη συνάρτηση f(x) = 1/(7-3*x)^5

Το αντιπαράγωγο για τη συνάρτηση 1/x^5 θα είναι η συνάρτηση (-1/(4*x^4)). Τώρα, χρησιμοποιώντας τον τρίτο κανόνα, παίρνουμε.