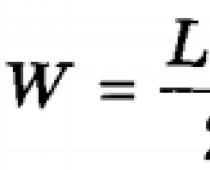Στόχος της εργασίας:αποκτήσουν πρακτικές δεξιότητες στη σύνταξη αλγορίθμων χρησιμοποιώντας τη σύνθεση μηχανών Turing.
Θεωρητικό υπόβαθρο
Οι παραπάνω μέθοδοι περιγραφής του MT μπορούν πρακτικά να χρησιμοποιηθούν μόνο για απλούς αλγόριθμους, διαφορετικά η περιγραφή γίνεται πολύ δυσκίνητη. Οι μηχανές Turing για σύνθετους αλγόριθμους μπορούν να κατασκευαστούν χρησιμοποιώντας τα ήδη υπάρχοντα στοιχειώδη MT, και μια τέτοια κατασκευή ονομάζεται σύνθεση ΜΤ.
Ας περιγράψουμε 4 βασικούς τρόπους σύνθεσης ΜΤ:
Διαδοχική σύνθεση (υπέρθεση);
Παράλληλη σύνθεση;
Διακλάδωση
1. Διαδοχική σύνθεση μηχανών Turing
Συνεπής σύνθεσηή προσθήκηΜηχανές Turing και 
Και 
στο αλφάβητο ΕΝΑ,κάλεσε το μηχάνημα Μ, που υπολογίζει τη συνάρτηση 
.
Η διαδοχική σύνθεση απεικονίζεται ως εξής:
και συμβολίζεται 
ή 
.
2. Παράλληλη σύνθεση μηχανών Turing
Παράλληλη σύνθεση
μηχανές 
Και 
, υπολογισμός συναρτήσεων λεξικού 
Και 
σε αλφάβητα ΕΝΑΚαι ΣΕ,αντίστοιχα, το όνομα του μηχανήματος Μ, που υπολογίζει τη συνάρτηση λεξικού . Εδώ υπογράψτε 
χρησιμοποιείται για τον διαχωρισμό λέξεων σε παράλληλη σύνθεση ΜΤ.
Παράλληλη σύνθεση ΜΤ 
Και 
απεικονίζεται ως εξής:
και συμβολίζεται: 
.
Στην πραγματικότητα, μια παράλληλη σύνθεση δύο MT λαμβάνει ως είσοδο μια λέξη που αποτελείται από 2 λέξεις σε διαφορετικά αλφάβητα και στην έξοδο παράγει μια λέξη που αποτελείται επίσης από 2 λέξεις, δηλ. αποτελείται από δύο μηχανές που λειτουργούν ταυτόχρονα και ανεξάρτητα. Για την υλοποίηση μιας παράλληλης σύνθεσης, χρησιμοποιείται ένα μηχάνημα με ταινία διπλού ορόφου.
Η μηχανή διπλής ταινίας λειτουργεί ως εξής:
1) λέξη 
ξαναγράφτηκε στον δεύτερο όροφο της ταινίας και σβήστηκε στον πρώτο,
2) υπολογισμένο 
στον πρώτο όροφο,
3) υπολογισμένο 
Στον δεύτερο όροφο
4)
ξαναγράφτηκε στον πρώτο όροφο, πιθανώς με μετατόπιση.
Η εντολή MT με ταινία διπλού ορόφου γράφεται ως εξής:
,
Οπου 
- επιστολές γραμμένες αντίστοιχα στον πρώτο και δεύτερο όροφο. Να δηλώσετε τη λέξη μήκη 
, αντίστοιχα, 
.
Θα δείξουμε τη λειτουργία της μηχανής Turing με μια ταινία διπλού ορόφου. Γενικά, μήκη λέξεων 
Και 
δεν συμπίπτουν μεταξύ τους, αλλά για απλότητα της εικόνας υποθέτουμε ότι είναι ίσα. Στη συνέχεια, η εφαρμογή των σημείων 1)-4) στο MT με μια διώροφη ταινία εκτελείται ως εξής:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Για την υλοποίηση παράλληλης σύνθεσης n Χρησιμοποιούνται μηχανές Turing n– ταινία δαπέδου.
3. Διακλάδωση ή διακλάδωση υπό όρους στη σύνθεση μηχανών Turing
Δίνονται μηχανές Turing 
Και 
, υπολογισμός συναρτήσεων λεξικού 
Και 
, και το μηχάνημα 
, το οποίο αξιολογεί κάποιο κατηγόρημα Π(
)
με ανάκτηση (δηλαδή χωρίς διαγραφή της λέξης
),
τότε μπορεί να κατασκευαστεί μια μηχανή Turing για την υλοποίηση της διακλάδωσης 
, που υπολογίζει τη συνάρτηση:
Η διακλάδωση των μηχανών Turing στα διαγράμματα σύνθεσης απεικονίζεται ως εξής:
και συμβολίζεται 
, Εδώ 
- το αποτέλεσμα του μηχανήματος 
, το οποίο παίρνει τις τιμές "1" εάν το κατηγόρημα Π(
)=
”αληθής”
και "0" αν το κατηγόρημα Π(
)=
“ψευδής”
,
είναι μια μηχανή Turing που υλοποιεί την αντιγραφή της λέξης εισόδου 
.
4 . Κύκλος στη σύνθεση των μηχανών Turing
Κύκλοςστη σύνθεση, το MT υλοποιείται σύμφωνα με τις ίδιες αρχές με τη διακλάδωση.
" Αντίο Π(
)=
”αληθής”
, εκπληρώνω 
»,
Οπου
- η λέξη στην κασέτα πριν από την πρώτη εκτέλεση 
και μετά την επόμενη εκτέλεση .
Για την εικόνα του κύκλου, εισάγουμε κάποια σημειογραφία, ας:
είναι μια μηχανή Turing που υλοποιεί τον υπολογισμό του κατηγορήματος Π(
)
;
–ΜΤ που υλοποιεί την αντιγραφή της λέξης εισόδου 
;
–ΜΤ, που εκτελείται σε κύκλο και πραγματοποιεί 
;
–MT, που εκτελείται κατά την έξοδο από τον βρόχο και την πραγματοποίηση 
.
Στη συνέχεια, η κυκλική σύνθεση των μηχανών Turing, ή κύκλος, μπορεί να απεικονιστεί ως εξής:
Προγραμματισμός με συνθέσεις μηχανών Turing:
1) κατασκευή μπλοκ διαγραμμάτων πολύπλοκων αλγορίθμων τέτοιου βαθμού λεπτομέρειας ώστε τα μπλοκ τους να αντιστοιχούν σε στοιχειώδεις ΜΤ.
2) κατασκευή στοιχειωδών ΜΤ που υλοποιούν απλά μπλοκ.
3) συνδυασμός στοιχειωδών ΜΤ σε μια σύνθεση ΜΤ.
Παράδειγμα.Κατασκευάστε μια σύνθεση ΜΤ που υλοποιεί 
.
– Μηχάνημα Turing που υλοποιεί την αντιγραφή της λέξης εισόδου.
–MT, το οποίο υλοποιεί τη συνάρτηση μηδενισμού της σταθεράς.
–ΜΤ υπολογιστικό κατηγόρημα με ανάκτηση 
;
– MT που υλοποιεί τη λειτουργία επιλογής 
-αυτό το επιχείρημα από 
επιχειρήματα
–MT, το οποίο υλοποιεί τη λειτουργία μείωσης του ορίσματος 
κατά 1 σε μονογενή κώδικα (διαγράφει τον αριστερό χαρακτήρα).
– ΜΤ που εκτελεί την πρόσθεση δύο αριθμών σε έναν ενιαίο κωδικό.
Θα πρέπει να σημειωθεί ότι σε κάθε περίπτωση, στην αρχή της εκτέλεσης του αλγορίθμου, είναι απαραίτητο να ελέγξετε τα δεδομένα εισόδου για ορθότητα (για παράδειγμα, την ισότητα του ορίσματος στο 0 κατά τη διαίρεση).
Η μηχανή Turing (MT) είναι ένας αφηρημένος εκτελεστής (abstract computing machine).
Συνδυασμοί αλγορίθμων είναι το όνομα που δίνεται σε έναν αριθμό συγκεκριμένων τρόπων κατασκευής νέων αλγορίθμων από πολλούς δεδομένους.
Τα θεωρήματα για συνδυασμούς αλγορίθμων αποτελούν σημαντικό μέρος της γενικής θεωρίας των αλγορίθμων. Έχοντας αποδειχθεί μία φορά, επιτρέπουν σε κάποιον να πειστεί στο μέλλον για τη σκοπιμότητα πολύπλοκων και δυσκίνητων αλγορίθμων χωρίς να γράψει πραγματικά τα σχήματα που τους καθορίζουν.
Οι συνδυασμοί αλγορίθμων για μια μηχανή Turing περιγράφονται από λειτουργίες σε μηχανές Turing.
1. Λειτουργία σύνθεσης.
Έστω M 1 και M 2 μηχανές Turing που έχουν το ίδιο εξωτερικό αλφάβητο A« (a 0 ,a 1 ,...,a p ). Ας συμβολίσουμε τα σύνολα των καταστάσεων τους ως Q1 « (q 0 ,q 1 ,...,q n ) και Q2 « (q 0" ,q 1" ,...,q m" ).
Ορισμός.
Μια σύνθεση των μηχανών M 1 και M 2 είναι μια μηχανή, που συμβολίζεται M=M 1 ×M 2 , της οποίας το πρόγραμμα έχει το αλφάβητο A, το σύνολο των καταστάσεων Q« (q 0 ,q 1 ,...,q n ,q n+1 ,...,q n+m ) και προκύπτει από τα προγράμματα των μηχανών , όπου τα προγράμματα των μηχανών Mw 2 ακολουθούν τα προγράμματα M 1 και τα M 1: " με το σύμβολο q 1 (η τελική κατάσταση της μηχανής M 1), αλλάζει στο σύμβολο q 0" (η αρχική κατάσταση της μηχανής M 2), όλα τα άλλα σύμβολα στα προγράμματα των μηχανών M 1 και M 2 παραμένουν αμετάβλητα (τελικά, μένει να αναριθμηθούν όλες οι καταστάσεις της μηχανής M: (q 0 ,q 1" ,q ,q ,q 2" ,q ,q 2" )).
Η σύνθεση αρχίζει να "λειτουργεί" σαν μια μηχανή M 1 , αλλά σε εκείνες τις περιπτώσεις που η μηχανή M 1 θα πρέπει να σταματήσει, υπάρχει αλλαγή στο πρόγραμμα της μηχανής M 2 λόγω αντικατάστασης του q 1 από q 0 ". Είναι προφανές ότι η λειτουργία σύνθεσης είναι συνειρμική, αλλά όχι ανταλλακτική.
Η λειτουργία του είναι ισοδύναμη με τη διαδοχική λειτουργία των μηχανών Τ1 και Τ2.
Το σχήμα δείχνει τη σύνθεση των μηχανών Turing που υλοποιεί τον τελεστή υπέρθεσης για n=1 και m=1.
Εικόνα 1.
Ορισμός.
Μια επανάληψη μιας μηχανής Turing M είναι η μηχανή
2. Λειτουργία υποκαταστήματος.
Έστω M 1 , M 2 και M 3 μηχανές Turing που έχουν το ίδιο εξωτερικό αλφάβητο A« (a 0 ,a 1 ,...,a i ,...,a j ,...,a p ) και, αντίστοιχα, σύνολα καταστάσεων: Q1 « (q 0 ,q 1 ,...,q n ), Q2 «, q" (q ) 1" ,... ,q l" ).
Ορισμός.
Το αποτέλεσμα της λειτουργίας διακλάδωσης στις μηχανές Turing M 1 , M 2 και M3 είναι η μηχανή Turing M, το πρόγραμμα της οποίας λαμβάνεται από τα προγράμματα των μηχανών M 1 , M 2 και M 3 ως εξής: γράφεται το πρόγραμμα της μηχανής M1 και στη συνέχεια εκχωρούνται τα προγράμματα της μηχανής M 2 και M 3. Εάν το σύμβολο a i παρατηρείται στην τελική κατάσταση q 1 της μηχανής M1, τότε ο έλεγχος μεταφέρεται στη μηχανή M 2 , δηλ. το σύμβολο q 1 αντικαθίσταται από το σύμβολο q 0" και η μηχανή M 2 αρχίζει να λειτουργεί. Εάν, ωστόσο, το σύμβολο a j παρατηρηθεί στην τελική κατάσταση q 1 της μηχανής M 1, τότε ο έλεγχος μεταφέρεται στη μηχανή M 3, δηλαδή το σύμβολο q 1 αντικαθίσταται από το σύμβολο q 0" και η μηχανή M 3 αρχίζει να λειτουργεί. Όλοι οι άλλοι χαρακτήρες στα προγράμματα των μηχανών M 1 και M 2 παραμένουν αμετάβλητοι. Το μηχάνημα M τερματίζει στην τελική κατάσταση q 1 (συμπερασματικά, μένει να πραγματοποιηθεί μια συνεχής αναμέτρηση των καταστάσεων της μηχανής M).
Το αποτέλεσμα της λειτουργίας διακλάδωσης στις μηχανές Turing M 1 , M 2 και M3 συμβολίζεται ως εξής:
Για μηχανές Turing δύο γραμμάτων (μηχανές Turing με αλφάβητο δύο γραμμάτων), η λειτουργία διακλάδωσης σε αυθαίρετες μηχανές Turing M1 , M2 και M3 συμβολίζεται ως εξής:
εκείνοι. εάν το σύμβολο a 0 παρατηρείται κατά τη λειτουργία της μηχανής M1 στην κατάσταση q 1 , τότε ο έλεγχος μεταφέρεται στη μηχανή M2 , διαφορετικά, στη μηχανή M3.
3. Ποδηλατική λειτουργία.
Έστω M μια μηχανή Turing με αλφάβητο A« (a 0 ,a 1 ,...,a p ) και σύνολο κατάστασης Q« (q 0 ,q 1 ,...,q n ).
Ορισμός.
Το αποτέλεσμα της λειτουργίας βρόχου θα ονομάζεται μηχανή Turing, που συμβολίζεται με (i=0,2,3,...,n; j=0,1,2,...,p; s=0,2,3,...,n)
του οποίου το πρόγραμμα προκύπτει από το πρόγραμμα της μηχανής M αντικαθιστώντας την εντολή q i a j ®q 1 a t r, rн(L,R,L), t=0,1,2,...p, το σύμβολο q 1 με το σύμβολο q s στο επακόλουθο e.
2.4 Παραλλαγές μηχανών Turing
Το μοντέλο μηχανής Turing επιτρέπει επεκτάσεις. Μπορεί κανείς να εξετάσει μηχανές Turing με αυθαίρετο αριθμό ταινιών και πολυδιάστατες ταινίες με διαφορετικούς περιορισμούς. Ωστόσο, όλες αυτές οι μηχανές είναι ολοκληρωμένες Turing και μοντελοποιούνται από μια κανονική μηχανή Turing.
Ως παράδειγμα μιας τέτοιας ισοδυναμίας, εξετάστε τη μείωση οποιουδήποτε ΜΤ σε ΜΤ που λειτουργεί σε μια ημι-άπειρη ταινία .
Θεώρημα:Για οποιαδήποτε μηχανή Turing, υπάρχει μια αντίστοιχη μηχανή Turing που λειτουργεί σε μια ημι-άπειρη ταινία.
Απόδειξη:
Εξετάστε την απόδειξη του Yu. G. Karpov. Η απόδειξη αυτού του θεωρήματος είναι εποικοδομητική, δηλαδή θα δώσουμε έναν αλγόριθμο με τον οποίο, για οποιαδήποτε μηχανή Turing, μπορεί να κατασκευαστεί μια ισοδύναμη μηχανή Turing με δηλωμένη ιδιότητα. Πρώτον, αριθμούμε αυθαίρετα τα κελιά της ταινίας εργασίας MT, δηλαδή προσδιορίζουμε τη νέα θέση των πληροφοριών στην ταινία:
Εικόνα 1.
Στη συνέχεια, επαναριθμούμε τα κελιά και θα υποθέσουμε ότι το σύμβολο "*" δεν περιέχεται στο λεξικό MT:
Εικόνα 1.
2.5 Υπολογισιμότητα και αποφασιστικότητα Turing
Αποδείχθηκε παραπάνω ότι οι κατηγορίες συναρτήσεων που μπορούν να υπολογιστούν χρησιμοποιώντας αναδρομικές συναρτήσεις, μηχανές Turing ή κανονικούς αλγόριθμους Markov συμπίπτουν. Αυτό μας επιτρέπει να θεωρήσουμε την έννοια του «υπολογιστικού αλγόριθμου» αμετάβλητη στη μέθοδο περιγραφής. Διαφορές παρατηρούνται μόνο στη χρήση αλγοριθμικών αντικειμένων. Εάν για τις αναδρομικές συναρτήσεις τα αντικείμενα είναι αριθμοί και αριθμητικές συναρτήσεις και η διαδικασία υπολογισμού καθορίζεται από τους τελεστές υπέρθεσης, αναδρομής, ελαχιστοποίησης και επανάληψης, τότε για τις μηχανές Turing τέτοια αντικείμενα είναι σύμβολα του αλφαβήτου της εξωτερικής και εσωτερικής μνήμης και η διαδικασία υπολογισμού καθορίζεται από το πρωτόκολλο χρησιμοποιώντας τη συνάρτηση εξόδου, μετάβασης και κίνησης κεφαλής. Για έναν κανονικό αλγόριθμο Markov, τέτοια αντικείμενα είναι λέξεις ή ακολουθίες χαρακτήρων και η διαδικασία υπολογισμού καθορίζεται από κανόνες αντικατάστασης ή προϊόντα που αλλάζουν τη σύνθεση και τη δομή της αρχικής ακολουθίας χαρακτήρων στο επιθυμητό αποτέλεσμα.
Αριθμητική (αριθμητική) συνάρτηση είναι μια συνάρτηση της οποίας το εύρος είναι υποσύνολο του συνόλου N και της οποίας το πεδίο ορισμού είναι στοιχείο του συνόλου N.
Για αλγοριθμικά προβλήματα, μια τυπική κατάσταση είναι όταν πρέπει να βρείτε έναν αλγόριθμο για τον υπολογισμό μιας αριθμητικής συνάρτησης f(x 1 , x 2 , ..., x n) ανάλογα με τις ακέραιες τιμές των ορισμάτων x 1 , x 2 , ..., x n .
Μια συνάρτηση f:N n →N ονομάζεται υπολογίσιμη εάν υπάρχει ένας αλγόριθμος που επιτρέπει σε οποιοδήποτε σύνολο τιμών των ορισμάτων της να υπολογίσει την τιμή της συνάρτησης (ή να υποδεικνύει ότι η συνάρτηση δεν ορίζεται σε αυτό το σύνολο). Δεδομένου ότι ο ορισμός μιας υπολογίσιμης συνάρτησης χρησιμοποιεί τη διαισθητική έννοια ενός αλγορίθμου, ο όρος "διαισθητικά υπολογίσιμη συνάρτηση" χρησιμοποιείται συχνά αντί του όρου "υπολογίσιμη συνάρτηση". Έτσι, ένα πρόβλημα μάζας έχει λύση εάν η αριθμητική συνάρτηση που αντιστοιχεί σε αυτό το πρόβλημα είναι διαισθητικά υπολογίσιμη.
Η συνάρτηση f(x 1 , x 2 , …, x n) ονομάζεται αποτελεσματικά υπολογίσιμη εάν για τις δεδομένες τιμές k 1 , k 2 , …, k n των ορισμάτων, μπορείτε να βρείτε την τιμή της συνάρτησης f(k 1 , k 2 , …,k n) χρησιμοποιώντας κάποια υπάρχουσα μηχανική διαδικασία (αλγόριθμος).
Αντί να αποσαφηνιστεί η έννοια του αλγορίθμου, μπορεί κανείς να εξετάσει μια τελειοποίηση της έννοιας της «υπολογίσιμης συνάρτησης». Συνήθως, ενεργούν με τον ακόλουθο τρόπο:
1. Εισάγεται μια ακριβώς καθορισμένη κατηγορία συναρτήσεων.
2. Βεβαιωθείτε ότι όλες οι συναρτήσεις από αυτήν την κλάση είναι υπολογίσιμες.
3. Αποδεχτείτε την υπόθεση (θέση) ότι η κλάση των υπολογίσιμων συναρτήσεων συμπίπτει με την εισαγόμενη κατηγορία συναρτήσεων.
Μια συνάρτηση ονομάζεται υπολογίσιμη εάν υπάρχει αλγόριθμος που την υπολογίζει. Η «υπολογισιμότητα» είναι μια από τις βασικές έννοιες της θεωρίας των αλγορίθμων, αμετάβλητη ως προς την υπολογισμένη συνάρτηση και τον αλγόριθμο. Η διαφορά μεταξύ μιας υπολογίσιμης συνάρτησης και ενός αλγορίθμου είναι η διαφορά μεταξύ της περιγραφής μιας συνάρτησης και του τρόπου με τον οποίο υπολογίζονται οι τιμές της δεδομένων των τιμών των ανεξάρτητων ορισμάτων.
διατριβή Turing. Οποιοσδήποτε διαισθητικός αλγόριθμος μπορεί να εφαρμοστεί χρησιμοποιώντας κάποια μηχανή Turing.
Από τη θέση του Turing προκύπτει ότι εάν προκύψουν αλγοριθμικά προβλήματα, τότε θα πρέπει να επιλυθούν με βάση την κατασκευή των μηχανών Turing, δηλαδή αρκεί μια τυπική ιδέα ενός αλγορίθμου. Επιπλέον, στα αλγοριθμικά προβλήματα συχνά δεν πρόκειται για την κατασκευή ενός αλγορίθμου, αλλά για τη δυνατότητα υπολογισμού ορισμένων συναρτήσεων που κατασκευάζονται με ειδικό τρόπο.
Πρέπει να σημειωθεί ότι σε αυτές τις περιπτώσεις αρκεί η χρήση του αλφαβήτου (0,|), όπου το 0 είναι κενός χαρακτήρας. Για παράδειγμα, οι φυσικοί αριθμοί, συμπεριλαμβανομένου του 0, κωδικοποιούνται σε αυτό το αλφάβητο ως εξής: 0 - |; 1 - ||; 2-
Ν - ||…| (n + 1 φορές). Μια μερική αριθμητική n τοπική συνάρτηση f(x1 , x2 , …, xn) ονομάζεται υπολογίσιμη Turing εάν υπάρχει μια μηχανή M που την υπολογίζει με την ακόλουθη έννοια: 1. Εάν το σύνολο των τιμών των ορισμάτων
ΤΟ ΠΡΟΒΛΗΜΑ ΤΗΣ ΑΥΤΟΕΦΑΡΜΟΓΗΣ
Σύμφωνα με τον ορισμό μιας μηχανής Turing, αυτό είναι το τριπλό Τ=
Π: τσιένα α ιένα ® q rένα όπως καιένα S tένα , a = 1, 2, …, k , Οπου S1-R, S2-ΜΕΓΑΛΟ, S3- ντο . (*)
Σε αυτή την περίπτωση, μπορούμε να υποθέσουμε ότι υπάρχουν μερικά κοινά αλφάβητα Α0Και Q0, στο οποίο γράφονται χαρακτήρες ένα Και q για όλες τις μηχανές Turing. Μετά τα σύμβολα τσιένα, α ιένα , q rένα, όπως καιένα, S tέναείναι σύμβολα αλφαβήτων Α0Και Q0.
Αυτή η προσέγγιση επιτρέπει σε όλες τις μηχανές Turing να αριθμούνται, δηλαδή να εκχωρούν σε κάθε μηχανή έναν συγκεκριμένο αριθμό (κωδικό) που είναι μοναδικός σε αυτή τη μηχανή, με τον οποίο θα ήταν δυνατή η διάκρισή της από άλλες μηχανές. Εδώ εξετάζουμε έναν από τους τρόπους αρίθμησης.
Αρίθμηση Gödel των μηχανών Turing. Αφήνω p1, p2, p3 , … - μια ακολουθία πρώτων αριθμών διατεταγμένων σε αύξουσα σειρά, για παράδειγμα, 2, 3, 5, 7, 11, 13, …
Αριθμός μηχανής Turing με πρόγραμμα (*)κάλεσε έναν αριθμό
n(T) = .
Παράδειγμα
Ένα μηχάνημα που υλοποιεί μια λειτουργία μικρό(Χ)= x + 1 , έχει πρόγραμμα στο αλφάβητο {0, } . Ο αριθμός αυτού του προγράμματος, λαμβάνοντας υπόψη το γεγονός ότι ένα 0 = 0 , Α'1= | ο αριθμός θα είναι:
n(T)= 2 1 3 1 5 1 7 1 11 1 13 1 17 0 19 0 23 1 29 3 .
Προφανώς, δεν είναι όλοι οι φυσικοί αριθμοί αριθμοί της μηχανής Turing. Από την άλλη, αν n είναι ο αριθμός ορισμένων μηχανών, σε γενικά αλφάβητα, τότε το πρόγραμμά του μπορεί να αποκατασταθεί μοναδικά από αυτόν τον αριθμό.
Αυτοκίνητο Τεφαρμόζεται στη λέξη n(Τ)(δηλαδή στον κωδικό του δικού σας αριθμού), που ονομάζεται αυτο-εφαρμοστέο .
Είναι δυνατή η κατασκευή μηχανών που μπορούν να εφαρμοστούν μόνοι τους και μηχανές που δεν μπορούν να εφαρμοστούν. Για παράδειγμα, το μηχάνημα από το συγκεκριμένο παράδειγμα είναι αυτο-εφαρμόσιμο. Αυτοκίνητο Τ, που δεν έχει χαρακτήρα διακοπής στα σωστά μέρη του προγράμματος (στο σώμα του πίνακα), δεν ισχύει για καμία λέξη και, κατά συνέπεια, για τη λέξη n(Τ).
Το πρόβλημα της αυτο-εφαρμογήςσυνίσταται στα εξής: να υποδείξει έναν αλγόριθμο που, δεδομένης οποιασδήποτε μηχανής Turing, θα καθόριζε εάν είναι αυτο-εφαρμόσιμος ή όχι.
Σύμφωνα με τη Θέση του Turing, ένας τέτοιος αλγόριθμος θα πρέπει να αναζητηθεί με τη μορφή μιας μηχανής Turing. Αυτό το μηχάνημα θα πρέπει να ισχύει για τους κωδικούς αριθμού όλων των μηχανών Turing και ανάλογα με το αποτέλεσμα της επεξεργασίας των κωδικών των δοκιμασμένων μηχανών, θα έχει διαφορετικές τελικές διαμορφώσεις.
Ας, για παράδειγμα, αυτό το αυτοκίνητο Τεφαρμόζεται στον κώδικα n(Τ * ) . Αν το μηχάνημα Τ * αυτο-εφαρμόζεται, στη συνέχεια η τελική διαμόρφωση του μηχανήματος Τέχει τη μορφή ένα" q0 | ΣΙ", και αν το μηχάνημα Τ * δεν είναι αυτοδύναμη, τότε η τελική διαμόρφωση του μηχανήματος Τέχει τη μορφή ένα" q0 0Β ". Εδώ α", Β", α", Β"- λέξεις.
ΘεώρημαΤο πρόβλημα της αυτο-εφαρμογής είναι αλγοριθμικά άλυτο, δηλαδή δεν υπάρχει μηχανή Turing που να λύνει αυτό το πρόβλημα με την παραπάνω έννοια.
Από το θεώρημα προκύπτει ότι δεν υπάρχει γενικός αλγόριθμος για την επίλυση του προβλήματος της αυτο-εφαρμογής. Σε συγκεκριμένες συγκεκριμένες περιπτώσεις, τέτοιοι αλγόριθμοι μπορεί να υπάρχουν.
Ας χρησιμοποιήσουμε τα αποτελέσματα αυτού του θεωρήματος για να αποδείξουμε τη μη αποφασιστικότητα του προβλήματος της εφαρμοσιμότητας στην αρχική λέξη.
Το πρόβλημα της εφαρμογής στην αρχική λέξη συνίσταται στα εξής: δημιουργία αλγόριθμου που, με μηχανή Τκαι λέξη Χ θα εγκαταστήσει, εφαρμοστέο μηχάνημα ΤΠαρεμπιπτόντως Χ ή όχι (αλλιώς ένα πρόβλημα διακοπής).
Όσον αφορά τις μηχανές Turing, παρόμοια με τη διατύπωση του προβλήματος της αυτο-εφαρμογής, αυτό το πρόβλημα διατυπώνεται ως εξής: είναι δυνατόν να κατασκευαστεί μια μηχανή που θα μπορούσε να εφαρμοστεί σε όλες τις λέξεις της μορφής n(Τ)0 Χ , Οπου Ττυχαία μηχανή, Χ είναι λέξη αυθαίρετη, και αν η μηχανή Τισχύει για τη λέξη Χ ένα" q0 |Β" , και αν το αυτοκίνητο Τδεν ισχύει για τη λέξη Χ , θα οδηγούσε στην τελική διαμόρφωση ένα" q0 0Β" . Εδώ α", Β"Και α", Β"- αυθαίρετες λέξεις.
ΘεώρημαΤο πρόβλημα της εφαρμογής στην αρχική λέξη είναι αλγοριθμικά άλυτο, δηλαδή δεν υπάρχει μηχανή Turing που να λύνει αυτό το πρόβλημα με την παραπάνω έννοια.
Όπως αναφέρθηκε παραπάνω για το πρόβλημα της αυτο-εφαρμογής, το πρώτο προκαταρκτικό βήμα είναι η αρίθμηση. Επομένως, παρακάτω αυτό το ζήτημα εξετάζεται και λύνεται με συνέπεια για τους αλγόριθμους και τους τρεις κύριους τύπους αλγοριθμικών μοντέλων.
Αρίθμηση αλγορίθμων
Η αρίθμηση των αλγορίθμων παίζει σημαντικό ρόλο στη μελέτη και ανάλυσή τους. Εφόσον οποιοσδήποτε αλγόριθμος μπορεί να προσδιοριστεί ως πεπερασμένη λέξη (που αναπαρίσταται ως πεπερασμένη ακολουθία συμβόλων κάποιου αλφαβήτου) και το σύνολο όλων των πεπερασμένων λέξεων σε ένα πεπερασμένο αλφάβητο είναι μετρήσιμο, τότε το σύνολο όλων των αλγορίθμων είναι επίσης μετρήσιμο. Αυτό σημαίνει την ύπαρξη αντιστοίχισης ένα προς ένα μεταξύ του συνόλου των φυσικών αριθμών και του συνόλου των αλγορίθμων, δηλαδή τη δυνατότητα ανάθεσης ενός αριθμού σε κάθε αλγόριθμο.
Η αρίθμηση των αλγορίθμων είναι ταυτόχρονα και η αρίθμηση όλων των αλγοριθμικά υπολογισμένων συναρτήσεων και κάθε συνάρτηση μπορεί να έχει άπειρο αριθμό αριθμών.
Η ύπαρξη αρίθμησης καθιστά δυνατή την εργασία με αλγόριθμους με τον ίδιο τρόπο όπως και με τους αριθμούς. Η αρίθμηση είναι ιδιαίτερα χρήσιμη στη μελέτη αλγορίθμων που λειτουργούν με άλλους αλγόριθμους.
Έστω ότι υπάρχει ένα ορισμένο πρόβλημα μάζας με ένα σύνολο αρχικών αντικειμένων X και ένα σύνολο επιθυμητών αντικειμένων Y. Για την ύπαρξη λύσης στο πρόβλημα μάζας, είναι απαραίτητο τα στοιχεία των συνόλων X και Y να είναι κατασκευαστικά αντικείμενα. Επομένως, τα στοιχεία αυτών των συνόλων μπορούν να απαριθμηθούν με φυσικούς αριθμούς. Έστω x∈ X κάποιο αρχικό αντικείμενο, συμβολίζουμε με n(x) τον αριθμό του. Αν στο πρόβλημα μάζας απαιτείται να ληφθεί το επιθυμητό αντικείμενο y∈ Y με τον αριθμό n(y) από το αρχικό αντικείμενο x, τότε ορίζουμε μια αριθμητική συνάρτηση f: Nn →N τέτοια ώστε f(n(x))=n(y).
Ως παράδειγμα κατασκευής αριθμητικών συναρτήσεων για προβλήματα μάζας, εξετάστε τα προβλήματα μάζας.
1. Εάν δίνεται ένας πίνακας ] φυσικών αριθμών, τότε μπορεί να συσχετιστεί με έναν φυσικό αριθμό 2x1, 3x2,... p(n)xn , όπου p(n) είναι ο ν-ος πρώτος αριθμός. Εξετάστε για παράδειγμα έναν πίνακα μήκους 5:
] 2x13x25x37x411x5.
Αυτή η αρίθμηση ορίζει την αριθμητική συνάρτηση f (για παράδειγμα, f(73500) = f(22315372110) = 20315272113 = 4891425).
2. Κάθε ρητός αριθμός έχει κάποιο φυσικό αριθμό. Η απαρίθμηση του συνόλου των επιθυμητών αντικειμένων του προβλήματος είναι ασήμαντη:
("ναι", "όχι") α (1, 0). Για ένα δεδομένο πρόβλημα μάζας, μπορείτε να δημιουργήσετε μια αριθμητική συνάρτηση ενός ορίσματος χρησιμοποιώντας το τέχνασμα από το προηγούμενο παράδειγμα ή μπορείτε να εξετάσετε μια συνάρτηση τριών ορισμάτων (τρεις αριθμοί στοιχείων του αρχικού τριπλού).
3. Η αρίθμηση των κειμένων του προγράμματος μπορεί να γίνει ως εξής: οποιοδήποτε πρόγραμμα μπορεί να γίνει αντιληπτό ως εγγραφή ενός αριθμού στο σύστημα αριθμών 256 (εάν χρησιμοποιήθηκαν οι χαρακτήρες του πίνακα ASCII για τη σύνταξη του προγράμματος).
Η μετάβαση από ένα πρόβλημα μάζας σε μια αριθμητική συνάρτηση μας επιτρέπει να μειώσουμε το ζήτημα της ύπαρξης λύσης στο πρόβλημα μάζας στο ζήτημα της ύπαρξης ενός αποτελεσματικού τρόπου υπολογισμού των τιμών μιας αριθμητικής συνάρτησης από τα ορίσματά της.
Αρίθμηση συνόλων αριθμών
Στη θεωρία των αλγορίθμων, έχει γίνει ευρέως διαδεδομένη μια τεχνική που καθιστά δυνατή τη μείωση της μελέτης συναρτήσεων πολλών μεταβλητών στη μελέτη συναρτήσεων μιας μεταβλητής. Βασίζεται στην απαρίθμηση των συνόλων αριθμών, έτσι ώστε να υπάρχει μια διπλή αντιστοιχία μεταξύ των συνόλων αριθμών και των αριθμών τους, και οι συναρτήσεις που καθορίζουν τον αριθμό του από ένα σύνολο αριθμών και από τον αριθμό του ίδιου του συνόλου αριθμών είναι γενικές αναδρομικές. Για παράδειγμα, για μια συνάρτηση που περιέχει δύο ανεξάρτητες μεταβλητές (x, y), αυτή η αντιστοίχιση h(x, y) μπορεί να μοιάζει με αυτό:
Εικόνα 1.
Έστω τα ζεύγη (x, y) να σχηματίσουν ένα μερικώς διατεταγμένο σύνολο N (2) . Δεδομένου h(x, y) = n, τότε υπάρχει μια αντίστροφη αντιστοίχιση: x = h -1 1 (n) και y= h -1 2 (n), δηλαδή h(h -1 1 (n), h -1 2 (n)) = n. Αυτό σας επιτρέπει να υπολογίσετε τον αριθμό n για οποιοδήποτε ζεύγος (x, y) και, αντίθετα, να υπολογίσετε τις τιμές των x και y από τον αριθμό n:
Χρησιμοποιώντας αυτούς τους κανόνες, μπορεί κανείς να υπολογίσει την αρίθμηση των τριπλών h 2 (x, y, z) = h(h(x, y), z) = n και, αντίθετα, με τον αριθμό του τριπλού - τις τιμές x, y, z. Για παράδειγμα, αν h 2 (x, y, z) = n, τότε z = h -1 2 (n), y = h -1 2 (h -1 1 (n)), x = h -1 1 (h -1 1 (n)), h 2 (x, y, z) = h (h -1 1 (h) (h -1 1 (h) (n) (n) (n) (n) -1 (n) (n) 1 (n) 1 (n) 1 (n) 1 (n)), h -1 2 (n)). Οι τριάδες (x, y, z) σχηματίζουν ένα μερικώς διατεταγμένο σύνολο N (3) . Ομοίως, για έναν αυθαίρετο αριθμό αριθμών έχουμε:
h n-1 (x1, x2,…, xn)=h(h…h(h(x1, x2), x3)… x n-1), xn). Αν h n-1 (x1, x2,…, xn)=m, τότε xn = h -1 2 (m), x n-1 =h -1 2 (h -1 1 (m)), ........................., x2 = h -1 2 (h -1 1 (...h -1 1 (m)...)), x1 = (h) (h)...
Έχοντας την αρίθμηση των συνόλων των συνόλων N (1) , N (2) ,..., N (i) ,..., N(n , όπου N (i) είναι το σύνολο των συνόλων (i) αριθμών, μπορούμε να καθορίσουμε μια συνδυασμένη αρίθμηση αυθαίρετων συνόλων αριθμών M = N (1) N (2) ... N (i) .. N(n, έχουμε N., x2) , = h(h n−1 (x1, x2,...,xn), n−1).
Αν h(x ,1x ,2..., x)n = m, τότε h n−1 (x ,1x ,2..., x)n = h -1 1 (m), n= h -1 2 (m)+1. Χρησιμοποιώντας τους παραπάνω τύπους, μπορείτε να ανακτήσετε τις τιμές των x1, x2,…, xn.
Παρόμοιες πληροφορίες.
Το διάγραμμα μοιάζει με γράφημα:
Τιμή πίνακα μηχανής
Τραπέζι 1
Μερικές λειτουργίες σε μηχανές Turing
Η λειτουργία της μηχανής Turing καθορίζεται πλήρως από τα αρχικά δεδομένα και το σύστημα εντολών. Ωστόσο, για να κατανοήσουμε πώς ένα συγκεκριμένο μηχάνημα λύνει ένα πρόβλημα, κατά κανόνα, χρειάζονται ουσιαστικές εξηγήσεις όπως αυτές που δίνονται για το μηχάνημα. 
. Αυτές οι εξηγήσεις μπορούν συχνά να γίνουν πιο επίσημες και ακριβείς χρησιμοποιώντας διαγράμματα ροής και ορισμένες λειτουργίες σε μηχανές Turing. Θυμηθείτε ότι η σύνθεση των συναρτήσεων 
Και 
ονομάζεται συνάρτηση 
, το οποίο λαμβάνεται με την εφαρμογή 
στο αποτέλεσμα του υπολογισμού 
. Ωστε να 
καθορίστηκε με αυτό 
, είναι απαραίτητο και επαρκές για 
καθορίστηκε στις 
, ΕΝΑ 
καθορίστηκε στις 
.
Θεώρημα 1. Αν 
Και 
είναι υπολογίσιμοι ο Τούρινγκ και στη συνέχεια η σύνθεσή τους 
είναι επίσης υπολογίσιμος ο Turing.
Αφήνω 
- μια μηχανή που υπολογίζει 
, ΕΝΑ 
- μια μηχανή που υπολογίζει 
, και το σύνολο των καταστάσεων τους, αντίστοιχα 
Και 
.
Ας φτιάξουμε ένα διάγραμμα μετάβασης της μηχανής 
από διαγράμματα 
Και 
ως εξής: προσδιορίστε την αρχική κορυφή 
διαγράμματα μηχανών 
με τελικό σημείο 
διαγράμματα μηχανών 
(για συστήματα εντολών, αυτό ισοδυναμεί με το γεγονός ότι το σύστημα εντολών 
αντιστοίχιση στο σύστημα εντολών 
και για αυτό 
σε ομάδες 
αντικατέστησε με 
). Παίρνουμε ένα διάγραμμα με ( 
) αναφέρει. αρχική κατάσταση 
ας ανακοινώσουμε 
και τελικό 
. Για απλότητα της σημειογραφίας, θα υποθέσουμε 
Και 
αριθμητικές συναρτήσεις μιας μεταβλητής.
Αφήνω 
ορίζεται. Επειτα 
Και
. Αυτοκίνητο 
θα περάσει από την ίδια ακολουθία διαμορφώσεων με τη διαφορά ότι αντί για 
θα περάσει μέσα 
. Αυτή η διαμόρφωση είναι η τυπική αρχική διαμόρφωση για το μηχάνημα. 
, Να γιατί 
. Αλλά αφού όλες οι ομάδες 
που περιέχονται σε 
, Οτι
και ως εκ τούτου 
. Αν 
δεν ορίζεται, λοιπόν 
ή 
δεν σταματά και, ως εκ τούτου, το μηχάνημα 
δεν θα σταματήσει. Το αυτοκίνητο λοιπόν 
υπολογίζει 
.
Το μηχάνημα κατασκευάστηκε με αυτόν τον τρόπο 
θα ονομαστεί σύνθεση μηχανών 
Και 
και ορίζουν 
(ή 
(
)), καθώς και να απεικονίσετε σε μπλοκ διάγραμμα:
Σύνθεση μηχανών Turing
Αφήνω 
,
,
- τρεις μηχανές Turing με το ίδιο εξωτερικό αλφάβητο 
, με αλφάβητα εσωτερικών καταστάσεων 
,
,
και προγράμματα 
,
,
αντίστοιχα.
Σύνθεση
μηχανές 
Και 
που ονομάζεται αυτοκίνητοΤ
, του οποίου το πρόγραμμα είναι η ένωση των συνόλων 
Και
, Οπου 
υποδηλώνει το σύνολο των εντολών που λαμβάνονται από 
αντικαθιστώντας όλα 
επί 
.
Πιρούνια μηχανής Turing
μηχανές διακλάδωσης
,
,
Με 
, συμβολικά
που ονομάζεται αυτοκίνητοΤ
, του οποίου το πρόγραμμα προκύπτει ως εξής: από 
εξαιρούνται οι εντολές 
Και 
Για 
, θα κληθεί το σύνολο που προκύπτει 
; Επειτα.
Μηχανή Turing Universal
Το σύνολο εντολών μιας μηχανής Turing μπορεί να ερμηνευτεί τόσο ως περιγραφή της λειτουργίας μιας συγκεκριμένης συσκευής όσο και ως πρόγραμμα, δηλ. ένα σύνολο συνταγών που αναμφίβολα οδηγούν σε ένα αποτέλεσμα. Κατά την ανάλυση παραδειγμάτων γίνεται άθελά της αποδεκτή η δεύτερη ερμηνεία, δηλ. ενεργούμε ως μηχανισμός που είναι σε θέση να αναπαράγει το έργο οποιασδήποτε μηχανής Turing. Η βεβαιότητα ότι θα το κάνουν όλοι με τον ίδιο τρόπο (αν δεν κάνουν λάθη, που, παρεμπιπτόντως, υποτίθεται και στη λειτουργία μιας μηχανής Turing) είναι ουσιαστικά η βεβαιότητα ότι υπάρχει ένας αλγόριθμος για την αναπαραγωγή της λειτουργίας μιας μηχανής Turing σύμφωνα με ένα δεδομένο πρόγραμμα, π.χ. σύστημα εντολών. Πράγματι, δεν είναι δύσκολο να δοθεί μια λεκτική περιγραφή ενός τέτοιου αλγορίθμου. Η κύρια δράση του είναι κυκλική και αποτελείται από τα εξής: «Για την τρέχουσα διαμόρφωση 
βρείτε στο σύστημα εντολών μια εντολή με την αριστερή πλευρά 
. Αν η δεξιά πλευρά αυτής της εντολής είναι 
, στη συνέχεια αντικαταστήστε την στην τρέχουσα διαμόρφωση 
επί 
(αποδεικνύεται η διαμόρφωση 
) αν η δεξιά πλευρά έχει τη μορφή 
, μετά αντικαταστήστε 
επί 
. Η λεκτική περιγραφή του αλγορίθμου μπορεί να είναι ανακριβής και πρέπει να επισημοποιηθεί. Εφόσον μια μηχανή Turing συζητείται τώρα ως μια τέτοια επισημοποίηση της έννοιας ενός αλγορίθμου, είναι φυσικό να τεθεί το πρόβλημα της κατασκευής μιας μηχανής Turing που υλοποιεί τον περιγραφόμενο αλγόριθμο αναπαραγωγής. Για τις μηχανές Turing που υπολογίζουν συναρτήσεις μιας μεταβλητής, η διατύπωση αυτού του προβλήματος είναι: κατασκευή μιας μηχανής Turing 
, που υπολογίζει μια συνάρτηση δύο μεταβλητών και τέτοια ώστε για οποιαδήποτε μηχανή 
με σύστημα εντολών 
, Αν 
ορίζεται (δηλαδή εάν η μηχανή 
σταματά στα αρχικά δεδομένα 
) Και 
δεν σταματά αν 
δεν σταματά. Κάθε μηχάνημα με την παραπάνω ιδιότητα θα καλείται universal μηχανή Turing. Είναι εύκολο να γενικευτεί αυτή η διατύπωση σε οποιονδήποτε αριθμό μεταβλητών.
Το πρώτο πρόβλημα που προκύπτει κατά την κατασκευή ενός καθολικού μηχανήματος 
, σχετίζεται με το γεγονός ότι 
όπως κάθε άλλη μηχανή Turing, πρέπει να έχει σταθερό αλφάβητο 
και ένα σταθερό σύνολο καταστάσεων 
. Επομένως, το σύστημα εντολών 
και τα αρχικά δεδομένα μιας αυθαίρετης μηχανής 
δεν μπορεί απλώς να μεταφερθεί στο μηχάνημα ταινίας 
(υπάρχει πάντα αυτοκίνητο 
, αλφάβητα 
Και 
που υπερτερεί σε δύναμη 
Και 
ή απλά δεν ταιριάζουν).
Η διέξοδος είναι στους χαρακτήρες από 
Και 
κωδικοποιούνται από χαρακτήρες στο αλφάβητο 
. Αφήνω 
,
. Πάντα θα το υποθέτουμε αυτό 
Και 
(αυτοί οι δύο χαρακτήρες είναι πάντα στο αλφάβητο κάθε μηχανής που λειτουργεί με αριθμούς). Σημειώστε τους κωδικούς 
Και 
διά μέσου 
Και 
και ορίστε τα ως 
; για οποιονδήποτε άλλον 
; για την τελική κατάσταση 
, Αν 
. Κώδικας 
για αυτό το μηχάνημα 
έχει πάντα μήκος (μορφή) 
, και τον κωδικό 
- μορφή 
. Σύμβολα 
,
ας εισαγάγουμε 
, δηλ. 
,
,
. Κωδικός συμβόλου 
, που σχηματίζονται από τους κωδικούς των χαρακτήρων που απαρτίζουν αυτή τη λέξη, δηλώνουν 
. Έτσι, η τελική τελειοποίηση της διατύπωσης του προβλήματος μιας καθολικής μηχανής 
καταλήγει στο γεγονός ότι για κάθε μηχανή 
και λέξεις 
αλφάβητο 
.
Η ύπαρξη μιας καθολικής μηχανής Turing σημαίνει ότι το σύνολο εντολών 
οποιοδήποτε αυτοκίνητο 
μπορεί να ερμηνευθεί με δύο τρόπους: είτε ως περιγραφή της λειτουργίας της αρχικής συσκευής 
, ή ως πρόγραμμα για ένα μηχάνημα γενικής χρήσης 
. Για έναν σύγχρονο μηχανικό που σχεδιάζει ένα σύστημα ελέγχου, αυτή η περίσταση είναι φυσική. Γνωρίζει καλά ότι οποιοσδήποτε αλγόριθμος ελέγχου μπορεί να εφαρμοστεί είτε σε υλικό - κατασκευάζοντας ένα κατάλληλο κύκλωμα, είτε σε λογισμικό - γράφοντας ένα πρόγραμμα για έναν καθολικό υπολογιστή ελέγχου.
Ωστόσο, είναι σημαντικό να συνειδητοποιήσουμε ότι η ιδέα μιας καθολικής αλγοριθμικής συσκευής είναι εντελώς άσχετη με την ανάπτυξη σύγχρονων τεχνικών μέσων για την υλοποίησή της (ηλεκτρονική, φυσική στερεάς κατάστασης, κ.λπ.) και δεν είναι ένα τεχνικό, αλλά ένα μαθηματικό γεγονός που περιγράφει με αφηρημένα μαθηματικούς όρους που δεν εξαρτώνται από τεχνικά μέσα και, επιπλέον, βασίζεται σε πολύ μικρό αρχικό στοιχείο. Είναι χαρακτηριστικό ότι οι θεμελιώδεις εργασίες για τη θεωρία των αλγορίθμων (ιδίως το έργο του Turing) εμφανίστηκαν στη δεκαετία του '30, πριν από τη δημιουργία των σύγχρονων υπολογιστών.
Αυτή η διπλή ερμηνεία διατηρεί σε αφηρημένο επίπεδο τα κύρια πλεονεκτήματα και τα μειονεκτήματα των δύο επιλογών για μηχανική υλοποίηση. μηχανή σκυροδέματος 
λειτουργεί πολύ πιο γρήγορα? επιπλέον, η συσκευή ελέγχου του μηχανήματος 
μάλλον δυσκίνητο (δηλαδή, ο αριθμός των καταστάσεων και των εντολών είναι μεγάλος). Ωστόσο, η τιμή του είναι σταθερή και, αφού κατασκευαστεί, είναι κατάλληλος για την υλοποίηση αυθαίρετα μεγάλων αλγορίθμων. Το μόνο που χρειάζεται είναι μια μεγάλη ποσότητα ταινίας, η οποία φυσικά θεωρείται φθηνότερη και πιο απλά τοποθετημένη από τη συσκευή ελέγχου. Επιπλέον, όταν αλλάζετε τον αλγόριθμο, δεν χρειάζεται να δημιουργήσετε νέες συσκευές, απλά πρέπει να γράψετε ένα νέο πρόγραμμα.
Εικόνα 1.6
Το Σχήμα 1.6 χρησιμοποιεί τον ακόλουθο συμβολισμό:
T 1, T 2 - Μηχανές Turing;
ST 1 , ST 2 - συστήματα εντολών μηχανών T 1 και T 2, αντίστοιχα.
x - αρχικές πληροφορίες για το μηχάνημα T 1 ;
T 1 (x) - το αποτέλεσμα της μηχανής T 1.
T 2 (T 1 (x)) - το αποτέλεσμα της εργασίας του μηχανήματος T 2.
Σκεφτείτε, για παράδειγμα, τη σύνθεση δύο μηχανών, η πρώτη από τις οποίες εκτελεί τη λειτουργία αντιγραφής και η δεύτερη - τη λειτουργία της προσθήκης αριθμών σε έναν ενιαίο κώδικα. Το σχήμα συνδυασμού μηχανών και ένα παράδειγμα ταινίας με τα αποτελέσματα που ελήφθησαν φαίνεται στο Σχήμα 1.7.
Εικόνα 1.7
Η σύνθεση που φαίνεται στο Σχήμα 1.7 σας επιτρέπει να εκτελέσετε τη λειτουργία του διπλασιασμού ενός αριθμού χρησιμοποιώντας ήδη γνωστά μηχανήματα αντιγραφής και προσθήκης. Έτσι, έχοντας καταρτίσει αλγόριθμους για μηχανές Turing για την επίλυση ενός συνόλου ορισμένων πράξεων (για παράδειγμα, αριθμητικές πράξεις), τότε μπορεί κανείς να συνθέσει μηχανές Turing για την επίλυση πιο περίπλοκων προβλημάτων. Ταυτόχρονα, η ανάπτυξη ενός γενικού αλγορίθμου περιορίζεται στη σύνταξη του από εκείνες τις λειτουργίες για τις οποίες είναι ήδη γνωστοί αλγόριθμοι για εκτέλεση σε μηχανή Turing. Αυτή η προσέγγιση είναι παρόμοια με τη χρήση διαδικασιών και συναρτήσεων στον προγραμματισμό.
Ωστόσο, η χρήση της σύνθεσης των μηχανών προϋποθέτει ότι είναι γνωστοί οι αλγόριθμοι για την εκτέλεση στοιχειωδών πράξεων, από τους οποίους αποτελείται ο γενικός αλγόριθμος. Επομένως, κατά την επίλυση αυθαίρετων προβλημάτων, αυτή η προσέγγιση δεν αποκλείει την ανάγκη ανάπτυξης νέων αλγορίθμων και, κατά συνέπεια, την ανάπτυξη μηχανών Turing με διαφορετικές μονάδες ελέγχου. Είναι δυνατή η υλοποίηση οποιουδήποτε αλγόριθμου χωρίς αλλαγή της δομής της μονάδας ελέγχου χρησιμοποιώντας τη μηχανή γενικής χρήσης Turing.
1.2.2 Μηχανή Turing Universal
Εάν δοθεί κάποια μηχανή Turing (δηλαδή, είναι γνωστά τα αλφάβητα εισόδου, σημάτων εξόδου και καταστάσεων, η αρχική θέση της κεφαλής και η αρχική κατάσταση της μηχανής, καθώς και ο πίνακας λειτουργίας της μηχανής και η ταινία με τις αρχικές πληροφορίες), τότε είναι δυνατό να εκτελεστούν χειροκίνητα όλες οι μετατροπές πληροφοριών για τις οποίες προορίζεται αυτό το μηχάνημα. Μάλιστα σε αυτή την περίπτωση γίνεται η προσομοίωση της μηχανής Turing.
Κατά την ανάλυση των λειτουργιών που εκτελούνται στην προσομοίωση μιας μηχανής Turing, μπορεί να διαπιστωθεί ότι η προσομοίωση περιορίζεται στην επανάληψη των ακόλουθων ενεργειών σε κάθε βήμα:
Ä Ανάγνωση ενός χαρακτήρα από το κελί της ταινίας πάνω στο οποίο βρίσκεται η κεφαλή.
ÄΑναζητήστε μια εντολή στον πίνακα χειρισμού του μηχανήματος. Η αναζήτηση εκτελείται από την τρέχουσα κατάσταση του μηχανήματος και την τιμή του χαρακτήρα ανάγνωσης.
ÄΕπιλέξτε από την εντολή τον χαρακτήρα που θα γραφτεί στην κασέτα και γράψτε τον.
ÄΕπιλογή του συμβόλου κίνησης της κεφαλής από την εντολή και μετακίνηση του.
ÄΕπιλογή νέας κατάστασης μηχανής από την εντολή και αλλαγή της τρέχουσας κατάστασης σε νέα. Ακολουθεί η μετάβαση στο επόμενο βήμα και η επανάληψη αυτών των βημάτων.
|
|
 |
|||||
 |
|||||
Εικόνα 1.8
Η φύση αυτών των στοιχειωδών λειτουργιών είναι τέτοια που μπορούν όλες να εκτελεστούν από κάποια άλλη μηχανή Turing που θα προσομοιώνει τη λειτουργία της αρχικής μηχανής. Η ουσία της μοντελοποίησης εξηγείται στο Σχήμα 1.8.
Εάν μια μηχανή T έχει ένα σύνολο εντολών ST και επεξεργάζεται μια ταινία με πληροφορίες X, τότε η λειτουργία της μπορεί να προσομοιωθεί από μια άλλη μηχανή U που έχει το δικό της σύνολο εντολών SU. Για την προσομοίωση, στην είσοδο του μηχανήματος U, είναι απαραίτητο να υποβάλετε όχι μόνο μια ταινία με πληροφορίες X , αλλά και το σύστημα εντολών (πίνακας εργασίας) ΣΤ. Αυτό το σύστημα εντολών μπορεί να εγγραφεί στην ίδια κασέτα με τις πρωτότυπες πληροφορίες.
 |
Εικόνα 1.9
Ένα σημαντικό χαρακτηριστικό της μηχανής προσομοίωσης είναι ότι το σύστημα εντολών SU (και, κατά συνέπεια, η δομή της μονάδας ελέγχου) δεν εξαρτάται από τον αλγόριθμο της προσομοιωμένης μηχανής Τ. Μια μηχανή Turing που μπορεί να προσομοιώσει τη λειτουργία οποιασδήποτε άλλης μηχανής Turing ονομάζεται καθολική. Μια παραλλαγή της δομής της καθολικής μηχανής Turing (UMT) φαίνεται στο Σχήμα 1.9.
Η ταινία UMT χωρίζεται σε τρεις ζώνες: τη ζώνη δεδομένων, τη ζώνη λειτουργίας και τη ζώνη εντολών.
Η ζώνη δεδομένων περιέχει τις αρχικές πληροφορίες προς επεξεργασία από την προσομοιωμένη μηχανή Turing. Στην ίδια ζώνη καταγράφονται τα αποτελέσματα των εργασιών του UMT.
Η ζώνη λειτουργίας περιέχει την τρέχουσα κατάσταση Q t και το τρέχον σύμβολο εισόδου X t που διαβάστηκε από το κελί της ζώνης δεδομένων σε έναν δεδομένο κύκλο.
Η ζώνη εντολών περιέχει το σύστημα εντολών για την προσομοιωμένη μηχανή. Οι εντολές ταξινομούνται σε ομάδες. Η πρώτη ομάδα περιλαμβάνει εντολές που ξεκινούν με τον χαρακτήρα Q 0 , η δεύτερη - με τον χαρακτήρα Q 1 και ούτω καθεξής. Σε κάθε ομάδα, οι εντολές ταξινομούνται με βάση την τιμή του χαρακτήρα X t . Έτσι, οι εντολές στην ταινία διατάσσονται όπως τοποθετούνται στον πίνακα λειτουργίας του προσομοιωμένου μηχανήματος.
Η ανάγνωση πληροφοριών από την ταινία και η εγγραφή στην κασέτα εκτελούνται χρησιμοποιώντας τρεις κεφαλές: D d - κεφαλή δεδομένων, G r - κεφαλή λειτουργίας, G c - κεφαλή εντολής. Κάθε κεφαλή μπορεί να κινηθεί στη δική της ζώνη της ταινίας.
Πριν από την έναρξη της λειτουργίας UMT, οι σχετικές πληροφορίες πρέπει να καταγράφονται σε κάθε ζώνη της ταινίας. Οι κεφαλές πρέπει να είναι τοποθετημένες πάνω από το αριστερό σύμβολο σε κάθε ζώνη.
Το έργο του UMT γίνεται σε κύκλους, σε κάθε κύκλο προσομοιώνεται η εκτέλεση μιας εντολής της προσομοιωμένης μηχανής. Το γράφημα εργασίας UMT φαίνεται στο Σχήμα 1.10.
 |
Εικόνα 1.10
Το Σχήμα 1.10 χρησιμοποιεί τον ακόλουθο συμβολισμό:
Q G σε P (G σε L, G r P, G r L, G d P, G d L) - μετακίνηση μιας από τις κεφαλές
δεξιά ή αριστερά;
Q (G έως), (G d), (G r) - πληροφορίες που διαβάζονται από έναν από τους επικεφαλής.
Q (G έως) à (G r) - ανάγνωση δεδομένων από την κεφαλή εντολών και εγγραφή αυτών των δεδομένων
χρησιμοποιώντας την κεφαλή λειτουργίας στην περιοχή λειτουργίας ταινίας.
Το Q a είναι μια βοηθητική μεταβλητή που παίρνει την τιμή 1, es-
εάν οι χαρακτήρες που διαβάζονται από τις κεφαλές Г έως και Г р συμπίπτουν.
Q in - μια βοηθητική μεταβλητή που παίρνει την τιμή 1, es-
εάν τα σύμβολα της τρέχουσας (Q t) και της τελικής (Q z) καταστάσεων είναι ίδια
Το Q p είναι ένα σήμα που παίρνει την τιμή 1 εάν η κεφαλή εντολής στο
η μετακίνηση προς τα αριστερά ξεπέρασε τα όρια της ζώνης διοίκησης.
Τα ακόλουθα βήματα εκτελούνται σε κάθε κύκλο UMT:
u αναζητήστε τη ζώνη εντολών.
u αναζήτηση για μια ομάδα στη ζώνη?
u προσομοίωση εκτέλεσης εντολών.
Η αναζήτηση ζώνης εντολών ξεκινά συγκρίνοντας την τρέχουσα κατάσταση Q t από τη ζώνη λειτουργίας με την κατάσταση Q i που καταγράφηκε στην αρχή της πρώτης εντολής στη ζώνη εντολών. Εάν αυτές οι καταστάσεις δεν είναι ίσες, τότε η κεφαλή εντολών μετακινείται στην αρχή της επόμενης εντολής, για την οποία εκτελούνται πέντε βήματα προς τα δεξιά (καταστάσεις U 0 - U 4). Εάν οι χαρακτήρες Q t και Q i ταιριάζουν, η κεφαλή των εντολών βρίσκεται στην αρχή της πρώτης εντολής της επιθυμητής ζώνης. Στη συνέχεια, ξεκινά η αναζήτηση για μια εντολή που αντιστοιχεί στα σύμβολα Q t και X t της ζώνης λειτουργίας. Για να γίνει αυτό, η κεφαλή λειτουργίας τοποθετείται πάνω από τον χαρακτήρα ζώνης λειτουργίας X t και η κεφαλή εντολών τοποθετείται πάνω από τον χαρακτήρα X i στην τρέχουσα εντολή.
Η αναζήτηση μιας ομάδας σε μια ζώνη εκτελείται με τον ίδιο τρόπο όπως η αναζήτηση μιας ζώνης ομάδας. Σε αυτήν την περίπτωση, η κεφαλή εντολών μετακινείται προς τα δεξιά κατά πέντε βήματα (καταστάσεις U 5 - U 9) μέχρι να συγκριθούν οι χαρακτήρες X t και X i.
Η εκτέλεση εντολών (καταστάσεις U 10 - U 17) ξεκινά με τη μετακίνηση της κεφαλής εντολών ένα βήμα προς τα δεξιά, μετά την οποία ο χαρακτήρας Y t που διαβάζεται από την εντολή που βρέθηκε γράφεται στη ζώνη δεδομένων χρησιμοποιώντας την κεφαλή δεδομένων αντί για τον προηγουμένως αναγνωσμένο χαρακτήρα X t . Μετά το επόμενο βήμα της κεφαλής εντολών προς τα δεξιά, το σύμβολο κίνησης της κεφαλής δεδομένων (Y d) διαβάζεται από την εντολή που βρέθηκε και η κεφαλή δεδομένων μετακινείται σύμφωνα με αυτό το σύμβολο (P, L). Κάτω από αυτόν είναι ο επόμενος επεξεργασμένος χαρακτήρας (X t +1), ο οποίος γράφεται στη ζώνη λειτουργίας με τη βοήθεια της κεφαλής λειτουργίας για την προετοιμασία του επόμενου κύκλου. Στη συνέχεια, οι κεφαλές εντολών και τρόπου λειτουργίας ορίζονται έτσι ώστε η επόμενη κατάσταση Q t +1 να μπορεί να γραφτεί στη ζώνη λειτουργίας (καταστάσεις
U 14, U 15). Στην κατάσταση U 16, ελέγχεται η προϋπόθεση για την καταγγελία της απόφασης. Εάν το σύμβολο της επόμενης κατάστασης δεν ταιριάζει με το σύμβολο της τελικής κατάστασης της προσομοιωμένης μηχανής (Q z), τότε η λύση του προβλήματος δεν ολοκληρώνεται και στην κατάσταση U 17 η κεφαλή εντολών μετακινείται στην αρχική της θέση (στην αρχή της πρώτης εντολής της πρώτης ζώνης). Σε αυτήν την περίπτωση, το UMT είναι έτοιμο να εκτελέσει τον επόμενο κύκλο, δηλ. για προσομοίωση της εκτέλεσης της επόμενης εντολής.
Εάν τα σύμβολα Q t και Q z συμπίπτουν, η λύση του προβλήματος τελειώνει και το UMT περνά στην τελική κατάσταση U z.
Κατά την ανάλυση της διαδικασίας λειτουργίας UMT, μπορεί να εξαχθεί ένα σημαντικό συμπέρασμα ότι ο αλγόριθμος της λειτουργίας UMT δεν εξαρτάται από το συγκεκριμένο πρόβλημα που επιλύει η προσομοιωμένη μηχανή Turing. Επομένως, η δομή της μονάδας ελέγχου UMT δεν αλλάζει κατά την προσομοίωση διαφόρων μηχανών, π.χ. δεν εξαρτάται από τις εργασίες που πρέπει να επιλυθούν. Γι' αυτό το UMT είναι πράγματι μια καθολική μηχανή με την οποία μπορεί να εκτελεστεί οποιοσδήποτε αλγόριθμος χωρίς να αλλάξει η δομή του.
Δεδομένου ότι η διαδικασία επιλογής της επόμενης εντολής UMT και η εκτέλεσή της συνδέεται με τη διαδοχική απαρίθμηση των κελιών της ταινίας, η επίλυση προβλημάτων στο UMT απαιτεί πάρα πολύ χρόνο. Ως εκ τούτου, η μηχανή Turing, συμπεριλαμβανομένης της καθολικής, δεν κατασκευάστηκε ποτέ, αλλά είναι εύκολο να δούμε σε αυτήν ένα ανάλογο των σύγχρονων υπολογιστών. Έτσι το σύστημα εντολών στη ζώνη εντολών UMT είναι παρόμοιο με το πρόγραμμα μηχανής, ενώ το ζεύγος συμβόλων Q t και X t παίζει το ρόλο της διεύθυνσης της εντολής μηχανής.
Ωστόσο, η μηχανή Turing είναι ένα αρκετά βολικό εργαλείο για την περιγραφή αλγορίθμων και χρησιμοποιείται ευρέως στη θεωρία των αλγορίθμων.
Ερωτήσεις ελέγχου
ü1.Ποια είναι η σύνθεση των μηχανών Turing;
ü2.Ποια είναι η σύνθεση των μηχανών Turing;
ü3. Μπορεί μια μηχανή Turing να προσομοιώσει τη λειτουργία μιας άλλης μηχανής
Turing;
ü4. Ποιες ενέργειες γίνονται σε αυτή την περίπτωση;
ü5.Εξηγήστε τη δομή της καθολικής μηχανής Turing;
ü6. Ποιες πληροφορίες καταγράφονται στις ζώνες της ταινίας UMT;
ü7.Τι είναι το σετ εντολών μηχανής Turing;
ü8. Ποια βήματα περιλαμβάνει ο κύκλος εργασίας UMT;
ü9.Εξηγήστε τα περιεχόμενα του βήματος «ζώνη εντολών αναζήτησης».
ü10.Εξηγήστε τα περιεχόμενα του βήματος "εκτέλεση εντολών".
ü11. Ποια είναι τα χαρακτηριστικά της διαδικασίας επεξεργασίας πληροφοριών που χρησιμοποιεί
- Σε επαφή με 0
- Google+ 0
- Εντάξει 0
- Facebook 0
