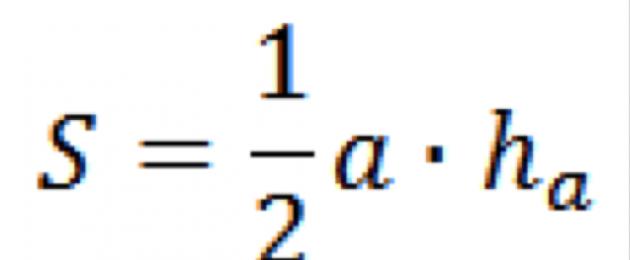Πώς να υπολογίσετε το εμβαδόν ενός σχήματος. Τύπος: περιοχή του δωματίου και οι διαστάσεις του Τύποι για τις περιοχές των κανονικών μορφών

Οι περιοχές των γεωμετρικών σχημάτων είναι αριθμητικές τιμές που χαρακτηρίζουν το μέγεθός τους σε δισδιάστατο χώρο. Αυτή η τιμή μπορεί να μετρηθεί σε μονάδες συστήματος και εκτός συστήματος. Έτσι, για παράδειγμα, μια μη συστημική μονάδα επιφάνειας είναι ένα εκατοστό, ένα εκτάριο. Αυτό συμβαίνει εάν η επιφάνεια που μετράται είναι ένα κομμάτι γης. Η μονάδα συστήματος εμβαδού είναι το τετράγωνο του μήκους. Στο σύστημα SI, η μονάδα εμβαδού επίπεδης επιφάνειας είναι το τετραγωνικό μέτρο. Στο GHS, η μονάδα εμβαδού εκφράζεται ως τετραγωνικό εκατοστό.

Οι τύποι γεωμετρίας και εμβαδού είναι άρρηκτα συνδεδεμένοι. Αυτή η σύνδεση έγκειται στο γεγονός ότι ο υπολογισμός των εμβαδών των επίπεδων ψηφίων βασίζεται ακριβώς στην εφαρμογή τους. Για πολλά σχήματα, προκύπτουν διάφορες επιλογές από τις οποίες υπολογίζονται οι τετραγωνικές τους διαστάσεις. Με βάση τα δεδομένα από τη δήλωση προβλήματος, μπορούμε να προσδιορίσουμε την απλούστερη δυνατή λύση. Αυτό θα διευκολύνει τον υπολογισμό και θα μειώσει την πιθανότητα σφαλμάτων υπολογισμού στο ελάχιστο. Για να το κάνετε αυτό, εξετάστε τις κύριες περιοχές των σχημάτων στη γεωμετρία.

Οι τύποι για την εύρεση της περιοχής οποιουδήποτε τριγώνου παρουσιάζονται σε διάφορες επιλογές:

1) Το εμβαδόν ενός τριγώνου υπολογίζεται από τη βάση α και το ύψος h. Ως βάση θεωρείται η πλευρά του σχήματος στην οποία χαμηλώνει το ύψος. Τότε το εμβαδόν του τριγώνου είναι:

2) Το εμβαδόν ενός ορθογώνιου τριγώνου υπολογίζεται με τον ίδιο τρόπο εάν η υποτείνουσα θεωρείται η βάση. Εάν πάρουμε το πόδι ως βάση, τότε το εμβαδόν του ορθογωνίου τριγώνου θα είναι ίσο με το γινόμενο των ποδιών που έχουν υποστεί κατά το ήμισυ.

Οι τύποι για τον υπολογισμό του εμβαδού οποιουδήποτε τριγώνου δεν τελειώνουν εκεί. Μια άλλη έκφραση περιέχει τις πλευρές a,b και την ημιτονοειδή συνάρτηση της γωνίας γ μεταξύ a και b. Η ημιτονοειδής τιμή βρίσκεται στους πίνακες. Μπορείτε επίσης να το μάθετε χρησιμοποιώντας μια αριθμομηχανή. Τότε το εμβαδόν του τριγώνου είναι:

Χρησιμοποιώντας αυτήν την ισότητα, μπορείτε επίσης να βεβαιωθείτε ότι το εμβαδόν ενός ορθογωνίου τριγώνου καθορίζεται μέσω των μήκων των ποδιών. Επειδή Η γωνία γ είναι μια ορθή γωνία, επομένως το εμβαδόν ενός ορθογωνίου τριγώνου υπολογίζεται χωρίς να πολλαπλασιαστεί με την ημιτονοειδή συνάρτηση.

3) Εξετάστε μια ειδική περίπτωση - ένα κανονικό τρίγωνο, του οποίου η πλευρά a είναι γνωστή από τη συνθήκη ή το μήκος του μπορεί να βρεθεί κατά την επίλυση. Τίποτα περισσότερο δεν είναι γνωστό για το σχήμα στο πρόβλημα της γεωμετρίας. Τότε πώς να βρείτε την περιοχή κάτω από αυτήν την κατάσταση; Σε αυτή την περίπτωση, εφαρμόζεται ο τύπος για το εμβαδόν ενός κανονικού τριγώνου:

Ορθογώνιο παραλληλόγραμμο

Πώς να βρείτε το εμβαδόν ενός ορθογωνίου και να χρησιμοποιήσετε τις διαστάσεις των πλευρών που έχουν κοινή κορυφή; Η έκφραση για τον υπολογισμό είναι:

Εάν πρέπει να χρησιμοποιήσετε τα μήκη των διαγωνίων για να υπολογίσετε το εμβαδόν ενός ορθογωνίου, τότε θα χρειαστείτε μια συνάρτηση του ημιτόνου της γωνίας που σχηματίζεται όταν τέμνονται. Αυτός ο τύπος για το εμβαδόν ενός ορθογωνίου είναι:

τετράγωνο

Το εμβαδόν ενός τετραγώνου προσδιορίζεται ως η δεύτερη δύναμη του μήκους της πλευράς:

Η απόδειξη προκύπτει από τον ορισμό ότι ένα τετράγωνο είναι ένα ορθογώνιο. Όλες οι πλευρές που σχηματίζουν ένα τετράγωνο έχουν τις ίδιες διαστάσεις. Επομένως, ο υπολογισμός του εμβαδού ενός τέτοιου ορθογωνίου καταλήγει στον πολλαπλασιασμό του ενός με το άλλο, δηλαδή στη δεύτερη δύναμη της πλευράς. Και ο τύπος για τον υπολογισμό του εμβαδού ενός τετραγώνου θα πάρει την επιθυμητή μορφή.

Το εμβαδόν ενός τετραγώνου μπορεί να βρεθεί με άλλο τρόπο, για παράδειγμα, εάν χρησιμοποιήσετε τη διαγώνιο:

Πώς να υπολογίσετε το εμβαδόν ενός σχήματος που σχηματίζεται από ένα τμήμα ενός επιπέδου που οριοθετείται από έναν κύκλο; Για τον υπολογισμό του εμβαδού, οι τύποι είναι:

Παραλληλόγραμμο

Για ένα παραλληλόγραμμο, ο τύπος περιέχει τις γραμμικές διαστάσεις της πλευράς, το ύψος και τη μαθηματική πράξη - πολλαπλασιασμό. Εάν το ύψος είναι άγνωστο, τότε πώς να βρείτε την περιοχή του παραλληλογράμμου; Υπάρχει άλλος τρόπος υπολογισμού. Θα απαιτηθεί μια ορισμένη τιμή, η οποία θα ληφθεί από την τριγωνομετρική συνάρτηση της γωνίας που σχηματίζουν οι γειτονικές πλευρές, καθώς και το μήκος τους.

Οι τύποι για το εμβαδόν ενός παραλληλογράμμου είναι:

Ρόμβος

Πώς να βρείτε το εμβαδόν ενός τετράπλευρου που ονομάζεται ρόμβος; Το εμβαδόν ενός ρόμβου προσδιορίζεται χρησιμοποιώντας απλά μαθηματικά με διαγώνιους. Η απόδειξη βασίζεται στο γεγονός ότι τα διαγώνια τμήματα στα d1 και d2 τέμνονται κάθετα. Ο πίνακας των ημιτόνων δείχνει ότι για μια ορθή γωνία αυτή η συνάρτηση είναι ίση με τη μονάδα. Επομένως, το εμβαδόν ενός ρόμβου υπολογίζεται ως εξής:

Η περιοχή ενός ρόμβου μπορεί επίσης να βρεθεί με άλλο τρόπο. Αυτό επίσης δεν είναι δύσκολο να αποδειχθεί, δεδομένου ότι οι πλευρές του έχουν το ίδιο μήκος. Στη συνέχεια, αντικαταστήστε το γινόμενο τους σε μια παρόμοια έκφραση για ένα παραλληλόγραμμο. Άλλωστε, μια ιδιαίτερη περίπτωση της συγκεκριμένης φιγούρας είναι ένας ρόμβος. Εδώ γ είναι η εσωτερική γωνία του ρόμβου. Το εμβαδόν ενός ρόμβου προσδιορίζεται ως εξής:

Τραπεζοειδές

Πώς να βρείτε την περιοχή ενός τραπεζοειδούς μέσω των βάσεων (α και β), εάν το πρόβλημα υποδεικνύει τα μήκη τους; Εδώ, χωρίς μια γνωστή τιμή του μήκους ύψους h, δεν θα είναι δυνατός ο υπολογισμός της περιοχής ενός τέτοιου τραπεζοειδούς. Επειδή Αυτή η τιμή περιέχει την έκφραση για τον υπολογισμό:

Η τετραγωνική διάσταση ενός ορθογώνιου τραπεζοειδούς μπορεί επίσης να υπολογιστεί με τον ίδιο τρόπο. Λαμβάνεται υπόψη ότι σε ένα ορθογώνιο τραπέζιο συνδυάζονται οι έννοιες του ύψους και της πλευράς. Επομένως, για ένα ορθογώνιο τραπεζοειδές, πρέπει να καθορίσετε το μήκος της πλευρικής πλευράς αντί για το ύψος.

Κύλινδρος και παραλληλεπίπεδο

Ας εξετάσουμε τι χρειάζεται για να υπολογίσουμε την επιφάνεια ολόκληρου του κυλίνδρου. Η περιοχή αυτού του σχήματος είναι ένα ζευγάρι κύκλων που ονομάζονται βάσεις και μια πλευρική επιφάνεια. Οι κύκλοι που σχηματίζουν κύκλους έχουν μήκη ακτίνας ίσες με r. Για το εμβαδόν ενός κυλίνδρου γίνεται ο ακόλουθος υπολογισμός:

Πώς να βρείτε την περιοχή ενός παραλληλεπίπεδου που αποτελείται από τρία ζεύγη όψεων; Οι μετρήσεις του ταιριάζουν με το συγκεκριμένο ζευγάρι. Οι απέναντι όψεις έχουν τις ίδιες παραμέτρους. Αρχικά, βρείτε S(1), S(2), S(3) - τις τετράγωνες διαστάσεις των άνισων όψεων. Τότε η επιφάνεια του παραλληλεπίπεδου είναι:

Δαχτυλίδι

Δύο κύκλοι με κοινό κέντρο σχηματίζουν έναν δακτύλιο. Περιορίζουν επίσης την περιοχή του δακτυλίου. Σε αυτήν την περίπτωση, και οι δύο τύποι υπολογισμού λαμβάνουν υπόψη τις διαστάσεις κάθε κύκλου. Το πρώτο από αυτά, υπολογίζοντας την περιοχή του δακτυλίου, περιέχει τις μεγαλύτερες ακτίνες R και μικρότερες r. Πιο συχνά ονομάζονται εξωτερικά και εσωτερικά. Στη δεύτερη έκφραση, η περιοχή του δακτυλίου υπολογίζεται μέσω των μεγαλύτερων διαμέτρων D και μικρότερων d. Έτσι, η περιοχή του δακτυλίου με βάση τις γνωστές ακτίνες υπολογίζεται ως εξής:

Η περιοχή του δακτυλίου, χρησιμοποιώντας τα μήκη των διαμέτρων, προσδιορίζεται ως εξής:

Πολύγωνο

Πώς να βρείτε το εμβαδόν ενός πολυγώνου του οποίου το σχήμα δεν είναι κανονικό; Δεν υπάρχει γενικός τύπος για την περιοχή τέτοιων αριθμών. Αλλά αν απεικονίζεται σε ένα επίπεδο συντεταγμένων, για παράδειγμα, θα μπορούσε να είναι καρό χαρτί, τότε πώς να βρείτε την επιφάνεια σε αυτήν την περίπτωση; Εδώ χρησιμοποιούν μια μέθοδο που δεν απαιτεί κατά προσέγγιση μέτρηση του σχήματος. Κάνουν αυτό: αν βρουν σημεία που εμπίπτουν στη γωνία του κελιού ή έχουν ολόκληρες συντεταγμένες, τότε μόνο αυτά λαμβάνονται υπόψη. Για να μάθετε στη συνέχεια ποια είναι η περιοχή, χρησιμοποιήστε τον τύπο που αποδείχθηκε από τον Peake. Είναι απαραίτητο να προσθέσετε τον αριθμό των σημείων που βρίσκονται μέσα στη διακεκομμένη γραμμή με τα μισά σημεία που βρίσκονται πάνω της και να αφαιρέσετε ένα, δηλ. υπολογίζεται ως εξής:

όπου B, G - ο αριθμός των σημείων που βρίσκονται εντός και σε ολόκληρη τη διακεκομμένη γραμμή, αντίστοιχα.

Εάν σχεδιάζετε να κάνετε μόνοι σας την ανακαίνιση, τότε θα χρειαστεί να κάνετε μια εκτίμηση για τα υλικά κατασκευής και φινιρίσματος. Για να γίνει αυτό, θα πρέπει να υπολογίσετε την περιοχή του δωματίου στο οποίο σκοπεύετε να πραγματοποιήσετε εργασίες ανακαίνισης. Ο κύριος βοηθός σε αυτό είναι μια ειδικά αναπτυγμένη φόρμουλα. Η περιοχή του δωματίου, δηλαδή ο υπολογισμός του, θα σας επιτρέψει να εξοικονομήσετε πολλά χρήματα για οικοδομικά υλικά και να κατευθύνετε τους ελευθερωμένους οικονομικούς πόρους προς μια πιο κατάλληλη κατεύθυνση.

Γεωμετρικό σχήμα του δωματίου

Ο τύπος για τον υπολογισμό της επιφάνειας ενός δωματίου εξαρτάται άμεσα από το σχήμα του. Τα πιο χαρακτηριστικά για τα οικιακά κτίρια είναι τα ορθογώνια και τετράγωνα δωμάτια. Ωστόσο, κατά την ανάπλαση, η τυπική φόρμα μπορεί να παραμορφωθεί. Τα δωμάτια είναι:

• Ορθογώνιος.
• Τετράγωνο.
• Σύνθετη διαμόρφωση (για παράδειγμα, στρογγυλή).
• Με κόγχες και προβολές.

Κάθε ένα από αυτά έχει τα δικά του χαρακτηριστικά υπολογισμού, αλλά, κατά κανόνα, χρησιμοποιείται ο ίδιος τύπος. Η περιοχή ενός δωματίου οποιουδήποτε σχήματος και μεγέθους, με τον ένα ή τον άλλο τρόπο, μπορεί να υπολογιστεί.

Ορθογώνιο ή τετράγωνο δωμάτιο

Για να υπολογίσετε το εμβαδόν ενός ορθογώνιου ή τετράγωνου δωματίου, απλώς θυμηθείτε τα μαθήματα γεωμετρίας του σχολείου σας. Επομένως, δεν θα πρέπει να είναι δύσκολο για εσάς να προσδιορίσετε την περιοχή του δωματίου. Ο τύπος υπολογισμού μοιάζει με:

S δωμάτια=A*B, όπου

Α είναι το μήκος του δωματίου.

B είναι το πλάτος του δωματίου.

Για να μετρήσετε αυτές τις τιμές θα χρειαστείτε μια κανονική μεζούρα. Για να έχετε τους πιο ακριβείς υπολογισμούς, αξίζει να μετρήσετε τον τοίχο και στις δύο πλευρές. Εάν οι τιμές δεν συμφωνούν, λάβετε ως βάση τον μέσο όρο των δεδομένων που προκύπτουν. Αλλά να θυμάστε ότι οποιοιδήποτε υπολογισμοί έχουν τα δικά τους σφάλματα, επομένως το υλικό πρέπει να αγοραστεί με αποθεματικό.

Ένα δωμάτιο με πολύπλοκη διαμόρφωση

Εάν το δωμάτιό σας δεν ταιριάζει με τον ορισμό του «τυπικού», π.χ. έχει σχήμα κύκλου, τριγώνου, πολυγώνου, τότε μπορεί να χρειαστείτε διαφορετικό τύπο για τους υπολογισμούς. Μπορείτε να προσπαθήσετε να διαιρέσετε κατά προσέγγιση την περιοχή ενός δωματίου με αυτό το χαρακτηριστικό σε ορθογώνια στοιχεία και να κάνετε υπολογισμούς χρησιμοποιώντας την τυπική μέθοδο. Εάν δεν έχετε αυτήν την ευκαιρία, χρησιμοποιήστε τις ακόλουθες μεθόδους:

• Τύπος εύρεσης του εμβαδού ενός κύκλου:

S room=π*R 2, όπου

R είναι η ακτίνα του δωματίου.

• Τύπος εύρεσης του εμβαδού ενός τριγώνου:

S δωμάτιο = √ (P(P - A) x (P - B) x (P - C)), όπου

P είναι η ημιπερίμετρος του τριγώνου.

Α, Β, Γ είναι τα μήκη των πλευρών του.

Επομένως P=A+B+C/2

Εάν έχετε οποιεσδήποτε δυσκολίες κατά τη διαδικασία υπολογισμού, τότε είναι καλύτερα να μην βασανίζετε τον εαυτό σας και να απευθυνθείτε σε επαγγελματίες.

Περιοχή του δωματίου με προβολές και κόγχες

Συχνά οι τοίχοι είναι διακοσμημένοι με διακοσμητικά στοιχεία με τη μορφή διαφόρων κόγχων ή προεξοχών. Επίσης, η παρουσία τους μπορεί να οφείλεται στην ανάγκη να κρύψετε κάποια αντιαισθητικά στοιχεία του δωματίου σας. Η παρουσία προεξοχών ή κόγχων στον τοίχο σας σημαίνει ότι ο υπολογισμός πρέπει να πραγματοποιείται σταδιακά. Εκείνοι. Αρχικά, βρίσκεται η περιοχή ενός επίπεδου τμήματος του τοίχου και στη συνέχεια προστίθεται η περιοχή της κόγχης ή της προεξοχής.

Η περιοχή του τοίχου βρίσκεται με τον τύπο:

S τοίχοι = P x C, όπου

P - περίμετρος

C - ύψος

Πρέπει επίσης να λάβετε υπόψη την παρουσία παραθύρων και θυρών. Το εμβαδόν τους πρέπει να αφαιρεθεί από την τιμή που προκύπτει.

Δωμάτιο με οροφή πολλαπλών επιπέδων

Ένα ανώτατο όριο πολλαπλών επιπέδων δεν περιπλέκει τους υπολογισμούς όσο φαίνεται με την πρώτη ματιά. Εάν έχει απλό σχεδιασμό, τότε οι υπολογισμοί μπορούν να γίνουν με βάση την αρχή της εύρεσης της περιοχής των τοίχων που περιπλέκονται από κόγχες και προβολές.

Ωστόσο, εάν το σχέδιο της οροφής σας έχει τοξωτά και κυματοειδή στοιχεία, τότε είναι πιο κατάλληλο να προσδιορίσετε την έκτασή του χρησιμοποιώντας την επιφάνεια του δαπέδου. Για να το κάνετε αυτό χρειάζεστε:

1. Βρείτε τις διαστάσεις όλων των ευθύγραμμων τμημάτων των τοίχων.
2. Βρείτε την επιφάνεια του δαπέδου.
3. Πολλαπλασιάστε το μήκος και το ύψος των κάθετων τμημάτων.
4. Αθροίστε την προκύπτουσα τιμή με την επιφάνεια του δαπέδου.

Βήμα προς βήμα οδηγίες για τον προσδιορισμό του γενικού

χώρο δωματίου

1. Καθαρίστε το δωμάτιο από περιττά πράγματα. Κατά τη διάρκεια της διαδικασίας μέτρησης, θα χρειαστείτε δωρεάν πρόσβαση σε όλους τους χώρους του δωματίου σας, επομένως πρέπει να απαλλαγείτε από οτιδήποτε μπορεί να παρεμβαίνει σε αυτό.
2. Διαχωρίστε οπτικά το δωμάτιο σε περιοχές κανονικού και ακανόνιστου σχήματος. Εάν το δωμάτιό σας έχει αυστηρά τετράγωνο ή ορθογώνιο σχήμα, τότε μπορείτε να παραλείψετε αυτό το βήμα.
3. Κάντε μια τυχαία διάταξη του δωματίου. Αυτό το σχέδιο είναι απαραίτητο ώστε όλα τα δεδομένα να είναι πάντα διαθέσιμα. Επίσης, δεν θα σας δώσει την ευκαιρία να μπερδευτείτε σε πολλές μετρήσεις.
4. Οι μετρήσεις πρέπει να γίνονται πολλές φορές. Αυτός είναι ένας σημαντικός κανόνας για την αποφυγή λαθών στους υπολογισμούς. Επίσης, εάν το χρησιμοποιείτε, βεβαιωθείτε ότι η δοκός βρίσκεται επίπεδη στην επιφάνεια του τοίχου.
5. Βρείτε τη συνολική επιφάνεια του δωματίου. Ο τύπος για τη συνολική επιφάνεια ενός δωματίου είναι να βρείτε το άθροισμα όλων των περιοχών των επιμέρους τμημάτων του δωματίου. Εκείνοι. S σύνολο = S τοίχοι+S δάπεδο+S οροφή

Για να λύσετε προβλήματα γεωμετρίας, πρέπει να γνωρίζετε τύπους - όπως το εμβαδόν ενός τριγώνου ή το εμβαδόν ενός παραλληλογράμμου - καθώς και απλές τεχνικές που θα καλύψουμε.

Αρχικά, ας μάθουμε τους τύπους για τις περιοχές των σχημάτων. Τα έχουμε συλλέξει ειδικά σε ένα βολικό τραπέζι. Εκτυπώστε, μάθετε και εφαρμόστε!

Φυσικά, δεν υπάρχουν όλοι οι τύποι γεωμετρίας στον πίνακά μας. Για παράδειγμα, για την επίλυση προβλημάτων γεωμετρίας και στερεομετρίας στο δεύτερο μέρος του προφίλ Unified State Exam στα μαθηματικά, χρησιμοποιούνται άλλοι τύποι για την περιοχή ενός τριγώνου. Σίγουρα θα σας πούμε για αυτούς.

Αλλά τι γίνεται αν δεν πρέπει να βρείτε την περιοχή ενός τραπεζοειδούς ή τριγώνου, αλλά την περιοχή μιας σύνθετης φιγούρας; Υπάρχουν καθολικοί τρόποι! Θα τους δείξουμε χρησιμοποιώντας παραδείγματα από την τράπεζα εργασιών FIPI.

1. Πώς να βρείτε την περιοχή μιας μη τυπικής φιγούρας; Για παράδειγμα, ένα αυθαίρετο τετράπλευρο; Μια απλή τεχνική - ας διαιρέσουμε αυτό το σχήμα σε εκείνα για τα οποία γνωρίζουμε τα πάντα και ας βρούμε το εμβαδόν του - ως το άθροισμα των εμβαδών αυτών των σχημάτων.

Διαιρέστε αυτό το τετράπλευρο με μια οριζόντια γραμμή σε δύο τρίγωνα με κοινή βάση ίση με . Τα ύψη αυτών των τριγώνων είναι ίσα Και . Τότε το εμβαδόν του τετράπλευρου είναι ίσο με το άθροισμα των εμβαδών των δύο τριγώνων: .

Απάντηση: .

2. Σε ορισμένες περιπτώσεις, το εμβαδόν ενός σχήματος μπορεί να αναπαρασταθεί ως η διαφορά ορισμένων περιοχών.

Δεν είναι τόσο εύκολο να υπολογίσεις με τι ισούται η βάση και το ύψος αυτού του τριγώνου! Μπορούμε όμως να πούμε ότι το εμβαδόν του είναι ίσο με τη διαφορά μεταξύ των εμβαδών ενός τετραγώνου με πλευρά και τρία ορθογώνια τρίγωνα. Τους βλέπετε στην εικόνα; Παίρνουμε: .

Απάντηση: .

3. Μερικές φορές σε μια εργασία πρέπει να βρείτε την περιοχή όχι ολόκληρης της φιγούρας, αλλά μέρος της. Συνήθως μιλάμε για το εμβαδόν ενός τομέα - μέρος ενός κύκλου Βρείτε το εμβαδόν ενός τομέα ενός κύκλου ακτίνας του οποίου το μήκος τόξου είναι ίσο με .

Σε αυτή την εικόνα βλέπουμε μέρος ενός κύκλου. Το εμβαδόν ολόκληρου του κύκλου είναι ίσο με . Απομένει να μάθουμε ποιο μέρος του κύκλου απεικονίζεται. Δεδομένου ότι το μήκος ολόκληρου του κύκλου είναι ίσο (από ), και το μήκος του τόξου ενός δεδομένου τομέα είναι ίσο , επομένως, το μήκος του τόξου είναι αρκετές φορές μικρότερο από το μήκος ολόκληρου του κύκλου. Η γωνία στην οποία στηρίζεται αυτό το τόξο είναι επίσης ένας παράγοντας μικρότερος από έναν πλήρη κύκλο (δηλαδή μοίρες). Αυτό σημαίνει ότι η περιοχή του τομέα θα είναι αρκετές φορές μικρότερη από την περιοχή ολόκληρου του κύκλου.

Υπολογισμός του εμβαδού ενός σχήματος- Αυτό είναι ίσως ένα από τα πιο δύσκολα προβλήματα στη θεωρία περιοχών. Στη σχολική γεωμετρία διδάσκονται να βρίσκουν τις περιοχές των βασικών γεωμετρικών σχημάτων όπως, για παράδειγμα, τρίγωνο, ρόμβος, ορθογώνιο, τραπέζιο, κύκλος κ.λπ. Ωστόσο, συχνά πρέπει να ασχοληθείτε με τον υπολογισμό των περιοχών των πιο περίπλοκων αριθμών. Κατά την επίλυση τέτοιων προβλημάτων είναι πολύ βολικό να χρησιμοποιείται ο ολοκληρωτικός λογισμός.

Ορισμός.

Καμπυλόγραμμο τραπεζοειδέςκαλέστε κάποιο σχήμα G που οριοθετείται από τις ευθείες y = f(x), y = 0, x = a και x = b, και η συνάρτηση f(x) είναι συνεχής στο τμήμα [a; β] και δεν αλλάζει το πρόσημά του σε αυτό (Εικ. 1).Η περιοχή ενός κυρτού τραπεζοειδούς μπορεί να συμβολιστεί με S(G).

Ένα οριστικό ολοκλήρωμα ʃ a b f(x)dx για τη συνάρτηση f(x), η οποία είναι συνεχής και μη αρνητική στο διάστημα [a; β], και είναι το εμβαδόν του αντίστοιχου κυρτού τραπεζοειδούς.

Δηλαδή, για να βρεθεί το εμβαδόν ενός σχήματος G που οριοθετείται από τις ευθείες y = f(x), y = 0, x = a και x = b, είναι απαραίτητο να υπολογιστεί το οριστικό ολοκλήρωμα ʃ a b f(x)dx .

Ετσι, S(G) = ʃ a b f(x)dx.

Αν η συνάρτηση y = f(x) δεν είναι θετική στο [a; b], τότε η περιοχή ενός καμπυλωμένου τραπεζοειδούς μπορεί να βρεθεί χρησιμοποιώντας τον τύπο S(G) = -ʃ a b f(x)dx.

Παράδειγμα 1.

Υπολογίστε το εμβαδόν του σχήματος που οριοθετείται από τις γραμμές y = x 3. y = 1; x = 2.

Λύση.

Οι δεδομένες γραμμές σχηματίζουν το σχήμα ABC, το οποίο φαίνεται με την εκκόλαψη ρύζι. 2.

Το απαιτούμενο εμβαδόν ισούται με τη διαφορά μεταξύ των περιοχών του κυρτού τραπεζοειδούς DACE και του τετραγώνου DABE.

Χρησιμοποιώντας τον τύπο S = ʃ a b f(x)dx = S(b) – S(a), βρίσκουμε τα όρια ολοκλήρωσης. Για να γίνει αυτό, λύνουμε ένα σύστημα δύο εξισώσεων:

(y = x 3,
(y = 1.

Έτσι, έχουμε x 1 = 1 – το κατώτερο όριο και x = 2 – το ανώτερο όριο.

Άρα, S = S DACE – S DABE = ʃ 1 2 x 3 dx – 1 = x 4 /4| 1 2 – 1 = (16 – 1)/4 – 1 = 11/4 (τετρ. μονάδες).

Απάντηση: 11/4 τ. μονάδες

Παράδειγμα 2.

Υπολογίστε το εμβαδόν του σχήματος που οριοθετείται από τις ευθείες y = √x. y = 2; x = 9.

Λύση.

Οι δοθείσες γραμμές σχηματίζουν το σχήμα ABC, το οποίο περιορίζεται παραπάνω από το γράφημα της συνάρτησης

y = √x, και παρακάτω είναι μια γραφική παράσταση της συνάρτησης y = 2. Το σχήμα που προκύπτει εμφανίζεται με εκκόλαψη σε ρύζι. 3.

Η απαιτούμενη περιοχή είναι S = ʃ a b (√x – 2). Ας βρούμε τα όρια της ολοκλήρωσης: b = 9, για να βρούμε το a, λύνουμε ένα σύστημα δύο εξισώσεων:

(y = √x,
(y = 2.

Έτσι, έχουμε ότι x = 4 = a - αυτό είναι το κατώτερο όριο.

Άρα, S = ∫ 4 9 (√x – 2)dx = ∫ 4 9 √x dx –∫ 4 9 2dx = 2/3 x√x| 4 9 – 2х| 4 9 = (18 – 16/3) – (18 – 8) = 2 2/3 (τετρ. μονάδες).

Απάντηση: S = 2 2/3 τετρ. μονάδες

Παράδειγμα 3.

Υπολογίστε το εμβαδόν του σχήματος που οριοθετείται από τις ευθείες y = x 3 – 4x. y = 0; x ≥ 0.

Λύση.

Ας σχεδιάσουμε τη συνάρτηση y = x 3 – 4x για x ≥ 0. Για να το κάνετε αυτό, βρείτε την παράγωγο y’:

y’ = 3x 2 – 4, y’ = 0 σε x = ±2/√3 ≈ 1,1 – κρίσιμα σημεία.

Αν σχεδιάσουμε τα κρίσιμα σημεία στην αριθμητική ευθεία και τακτοποιήσουμε τα πρόσημα της παραγώγου, διαπιστώνουμε ότι η συνάρτηση μειώνεται από το μηδέν στο 2/√3 και αυξάνεται από το 2/√3 στο συν άπειρο. Τότε x = 2/√3 είναι το ελάχιστο σημείο, η ελάχιστη τιμή της συνάρτησης y min = -16/(3√3) ≈ -3.

Ας προσδιορίσουμε τα σημεία τομής του γραφήματος με τους άξονες συντεταγμένων:

αν x = 0, τότε y = 0, που σημαίνει ότι το A(0; 0) είναι το σημείο τομής με τον άξονα Oy.

αν y = 0, τότε x 3 – 4x = 0 ή x(x 2 – 4) = 0, ή x(x – 2)(x + 2) = 0, από όπου x 1 = 0, x 2 = 2, x 3 = -2 (δεν είναι κατάλληλο, γιατί x ≥ 0).

Τα σημεία A(0; 0) και B(2; 0) είναι τα σημεία τομής της γραφικής παράστασης με τον άξονα Ox.

Οι δεδομένες γραμμές σχηματίζουν το σχήμα OAB, το οποίο φαίνεται με την εκκόλαψη ρύζι. 4.

Εφόσον η συνάρτηση y = x 3 – 4x παίρνει αρνητική τιμή στο (0; 2), τότε

S = |ʃ 0 2 (x 3 – 4x)dx|.

Έχουμε: ʃ 0 2 (x 3 – 4х)dx =(x 4 /4 – 4х 2 /2)| 0 2 = -4, από όπου S = 4 τετρ. μονάδες

Απάντηση: S = 4 τετρ. μονάδες

Παράδειγμα 4.

Βρείτε το εμβαδόν του σχήματος που οριοθετείται από την παραβολή y = 2x 2 – 2x + 1, τις ευθείες x = 0, y = 0 και την εφαπτομένη αυτής της παραβολής στο σημείο με την τετμημένη x 0 = 2.

Λύση.

Αρχικά, ας δημιουργήσουμε μια εξίσωση για την εφαπτομένη της παραβολής y = 2x 2 – 2x + 1 στο σημείο με την τετμημένη x₀ = 2.

Εφόσον η παράγωγος y’ = 4x – 2, τότε για x 0 = 2 παίρνουμε k = y’(2) = 6.

Ας βρούμε την τεταγμένη του εφαπτομένου σημείου: y 0 = 2 2 2 – 2 2 + 1 = 5.

Επομένως, η εφαπτομενική εξίσωση έχει τη μορφή: y – 5 = 6 (x ∙ – 2) ή y = 6x – 7.

Ας φτιάξουμε ένα σχήμα που οριοθετείται από γραμμές:

y = 2x 2 – 2x + 1, y = 0, x = 0, y = 6x – 7.

Г у = 2х 2 – 2х + 1 – παραβολή. Σημεία τομής με τους άξονες συντεταγμένων: A(0; 1) – με τον άξονα Oy. με τον άξονα Ox - δεν υπάρχουν σημεία τομής, γιατί η εξίσωση 2x 2 – 2x + 1 = 0 δεν έχει λύσεις (Δ< 0). Найдем вершину параболы:

x b = 2/4 = 1/2;

y b = 1/2, δηλαδή η κορυφή του σημείου της παραβολής Β έχει συντεταγμένες B(1/2; 1/2).

Έτσι, το σχήμα του οποίου το εμβαδόν πρέπει να προσδιοριστεί εμφανίζεται με εκκόλαψη ρύζι. 5.

Έχουμε: S O A B D = S OABC – S ADBC.

Ας βρούμε τις συντεταγμένες του σημείου Δ από την συνθήκη:

6x – 7 = 0, δηλ. x = 7/6, που σημαίνει DC = 2 – 7/6 = 5/6.

Βρίσκουμε την περιοχή του τριγώνου DBC χρησιμοποιώντας τον τύπο S ADBC ​​= 1/2 · DC · BC. Ετσι,

S ADBC ​​= 1/2 · 5/6 · 5 = 25/12 τετρ. μονάδες

S OABC = ʃ 0 2 (2x 2 – 2x + 1)dx = (2x 3 /3 – 2x 2 /2 + x)| 0 2 = 10/3 (τετρ. μονάδες).

Τελικά παίρνουμε: S O A B D = S OABC – S ADBC ​​· = 10/3 – 25/12 = 5/4 = 1 1/4 (τετρ. μονάδες).

Απάντηση: S = 1 1/4 τετρ. μονάδες

Εξετάσαμε παραδείγματα βρίσκοντας τα εμβαδά των σχημάτων που οριοθετούνται από δεδομένες γραμμές. Για να επιλύσετε με επιτυχία τέτοια προβλήματα, πρέπει να είστε σε θέση να κατασκευάζετε γραμμές και γραφήματα συναρτήσεων σε ένα επίπεδο, να βρίσκετε τα σημεία τομής των γραμμών, να εφαρμόζετε έναν τύπο για να βρείτε την περιοχή, που υποδηλώνει τη δυνατότητα υπολογισμού ορισμένων ολοκληρωμάτων.

ιστοσελίδα, όταν αντιγράφετε υλικό εν όλω ή εν μέρει, απαιτείται σύνδεσμος προς την πηγή.

Εμβαδόν γεωμετρικού σχήματος- ένα αριθμητικό χαρακτηριστικό ενός γεωμετρικού σχήματος που δείχνει το μέγεθος αυτού του σχήματος (τμήμα της επιφάνειας που περιορίζεται από το κλειστό περίγραμμα αυτού του σχήματος). Το μέγεθος του εμβαδού εκφράζεται με τον αριθμό των τετραγωνικών μονάδων που περιέχονται σε αυτό.

Τύποι τριγωνικού εμβαδού

1. Τύπος για το εμβαδόν ενός τριγώνου δίπλα και το ύψος
   Εμβαδόν τριγώνουίσο με το μισό γινόμενο του μήκους μιας πλευράς ενός τριγώνου και του μήκους του υψομέτρου που τραβιέται σε αυτήν την πλευρά
   
2. Τύπος για το εμβαδόν ενός τριγώνου που βασίζεται σε τρεις πλευρές και την ακτίνα του κυκλικού κύκλου
   
3. Τύπος για το εμβαδόν ενός τριγώνου που βασίζεται σε τρεις πλευρές και την ακτίνα του εγγεγραμμένου κύκλου
   Εμβαδόν τριγώνουισούται με το γινόμενο της ημιπεριμέτρου του τριγώνου και της ακτίνας του εγγεγραμμένου κύκλου.
   
όπου S είναι το εμβαδόν του τριγώνου,
- τα μήκη των πλευρών του τριγώνου,
- ύψος του τριγώνου,
- η γωνία μεταξύ των πλευρών και,
- ακτίνα του εγγεγραμμένου κύκλου,
R - ακτίνα του περιγεγραμμένου κύκλου,

Τύποι τετραγωνικού εμβαδού

1. Τύπος για το εμβαδόν ενός τετραγώνου κατά μήκος της πλευράς
   Τετράγωνη έκτασηίσο με το τετράγωνο του μήκους της πλευράς του.
2. Τύπος για το εμβαδόν ενός τετραγώνου κατά μήκος της διαγώνιας
   Τετράγωνη έκτασηίσο με το μισό του τετραγώνου του μήκους της διαγωνίου του.
   

   S=	1	2
   	2

όπου S είναι το εμβαδόν του τετραγώνου,
- μήκος της πλευράς του τετραγώνου,
- μήκος της διαγωνίου του τετραγώνου.

Τύπος ορθογώνιου εμβαδού

Εμβαδόν ορθογωνίουίσο με το γινόμενο των μηκών των δύο διπλανών πλευρών του

όπου S είναι το εμβαδόν του ορθογωνίου,
- μήκη των πλευρών του ορθογωνίου.

Τύποι εμβαδού παραλληλογράμμου

1. Τύπος για το εμβαδόν ενός παραλληλογράμμου με βάση το μήκος και το ύψος της πλευράς
   Εμβαδόν παραλληλογράμμου
2. Τύπος για το εμβαδόν ενός παραλληλογράμμου με βάση δύο πλευρές και τη γωνία μεταξύ τους
   Εμβαδόν παραλληλογράμμουισούται με το γινόμενο των μηκών των πλευρών του πολλαπλασιασμένο με το ημίτονο της μεταξύ τους γωνίας.
   

   α β αμαρτία α

όπου S είναι το εμβαδόν του παραλληλογράμμου,
- τα μήκη των πλευρών του παραλληλογράμμου,
- μήκος παραλληλογράμμου ύψους,
- η γωνία μεταξύ των πλευρών του παραλληλογράμμου.

Τύποι για την περιοχή ενός ρόμβου

1. Τύπος για το εμβαδόν ενός ρόμβου με βάση το μήκος και το ύψος της πλευράς
   Περιοχή ρόμβουίσο με το γινόμενο του μήκους της πλευράς του και το μήκος του ύψους που έχει χαμηλώσει σε αυτήν την πλευρά.
2. Τύπος για το εμβαδόν ενός ρόμβου με βάση το μήκος και τη γωνία της πλευράς
   Περιοχή ρόμβουείναι ίσο με το γινόμενο του τετραγώνου του μήκους της πλευράς του και του ημιτόνου της γωνίας μεταξύ των πλευρών του ρόμβου.
3. Τύπος για το εμβαδόν ενός ρόμβου με βάση τα μήκη των διαγωνίων του
   Περιοχή ρόμβουίσο με το μισό του γινόμενου των μηκών των διαγωνίων του.
όπου S είναι το εμβαδόν του ρόμβου,
- μήκος της πλευράς του ρόμβου,
- μήκος του ύψους του ρόμβου,
- η γωνία μεταξύ των πλευρών του ρόμβου,
1, 2 - μήκη διαγωνίων.

Τύποι τραπεζοειδούς περιοχής

1. Ο τύπος του Heron για το τραπεζοειδές

   Όπου S είναι το εμβαδόν του τραπεζοειδούς,
   - τα μήκη των βάσεων του τραπεζοειδούς,
   - μήκη των πλευρών του τραπεζοειδούς,